
【题目】(本题满分15分)已知中心在原点O,焦点在x轴上,离心率为![]() 的椭圆过点(
的椭圆过点(![]() ,
,![]() ).
).
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.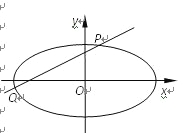
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(Ⅰ) 解:由题意可设椭圆方程为![]() (a>b>0),
(a>b>0),
则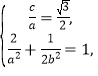 故
故![]()
所以,椭圆方程为![]() . ……………………………5分
. ……………………………5分
(Ⅱ) 解:由题意可知,直线l的斜率存在且不为0,
故可设直线l的方程为y=kx+m(m≠0),P(x1,y1),Q(x2,y2),
由![]() 消去y得
消去y得
(1+4k2)x2+8kmx+4(m2-1)=0,
则Δ=64k2b2-16(1+4k2b2)(b2-1)=16(4k2-m2+1)>0,
且![]() ,
,![]() .
.
故 y1 y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.
因为直线OP,PQ,OQ的斜率依次成等比数列,
所以![]() =
=![]() =k2,
=k2,
即![]() +m2=0,又m≠0,
+m2=0,又m≠0,
所以k2=![]() ,即k=
,即k=![]() .
.
由于直线OP,OQ的斜率存在,且Δ>0,得
0<m2<2 且m2≠1.
设d为点O到直线l的距离,
则S△OPQ=![]() d |PQ |=
d |PQ |=![]() |x1-x2 | |m |=
|x1-x2 | |m |=![]() ,
,
所以S△OPQ的取值范围为 (0,1). ……………………………15分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了调查教师对教育改革认识水平,现从某市年龄在![]() 的教师队伍中随机选取100名教师,得到的频率分布直方图如图所示,若从年龄在
的教师队伍中随机选取100名教师,得到的频率分布直方图如图所示,若从年龄在![]() 中用分层抽样的方法选取6名教师代表.
中用分层抽样的方法选取6名教师代表.

(1)求年龄在![]() 中的教师代表人数;
中的教师代表人数;
(2)在这6名教师代表中随机选取2名教师,求在![]() 中至少有一名教师被选中的概率.
中至少有一名教师被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某工厂要设计一个部件(如图阴影部分所示),要求从圆形铁片上进行裁剪,部件由三个全等的矩形和一个等边三角形构成,设矩形的两边长分别为![]() ,
,![]() (单位:cm),且要求
(单位:cm),且要求![]() ,部件的面积是
,部件的面积是![]() .
.

(1)求y关于x的函数表达式,并求定义域;
(2)为了节省材料,请问x取何值时,所用到的圆形铁片面积最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求与直线3x+4y-7=0垂直,且与原点的距离为6的直线方程;
(2)求经过直线l1:2x+3y-5=0与l2:7x+15y+1=0的交点,且平行于直线x+2y-3=0的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园举办雕塑展览吸引着四方宾客,旅游人数![]() 与人均消费
与人均消费![]() (元)的关系如下:
(元)的关系如下: .
.
(1)若游客客源充足,那么当天接待游客多少人时,公园的旅游收入最多?
(2)若公园每天运营成本为5万元(不含工作人员的工资),还要上缴占旅游收入![]() 的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,过椭圆的左焦点
,过椭圆的左焦点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相交所得弦长为
相交所得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,若存在,求直线
,若存在,求直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com