
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点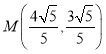 在椭圆C上,延长
在椭圆C上,延长![]() 交椭圆于N点.
交椭圆于N点.
(1)求椭圆C的方程;
(2)P,Q为椭圆上的点,记线段MN,PQ的中点分别为A,B(A,B异于原点O),且直线AB过原点O,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式(4kx﹣k2﹣12k﹣9)(2x﹣11)>0,其中k∈R,对于不等式的解集A,记B=A∩Z(其中Z为整数集),若集合B是有限集,则使得集合B中元素个数最少时的实数k的取值范围是__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是_________(请把你认为正确说法的序号都填上).
(1)函数![]() 的最小正周期为
的最小正周期为![]()
(2)若命题![]() :“
:“![]() ,使得
,使得![]() ”,则
”,则![]() :“
:“![]() ,均有
,均有![]() ”
”
(3)![]() 中,
中,![]() 是
是![]() 的充要条件;
的充要条件;
(4)已知点N在![]() 所在平面内,且
所在平面内,且![]() ,则点N是
,则点N是![]() 的重心;
的重心;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在集合![]() 的子集中选出4个不同的子集,需同时满足以下两个条件:
的子集中选出4个不同的子集,需同时满足以下两个条件:
(1)![]() ,
,![]() 都要选出;(2)对选出的任意两个子集
都要选出;(2)对选出的任意两个子集![]() 和
和![]() ,必有
,必有![]() 或
或![]() ;
;
那么具有_______种不同的选法;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用平面截圆柱面,当圆柱的轴与![]() 所成角为锐角时,圆柱面的截面是一个椭圆,著名数学家
所成角为锐角时,圆柱面的截面是一个椭圆,著名数学家![]() 创立的双球实验证明了上述结论.如图所示,将两个大小相同的球嵌入圆柱内,使它们分别位于
创立的双球实验证明了上述结论.如图所示,将两个大小相同的球嵌入圆柱内,使它们分别位于![]() 的上方和下方,并且与圆柱面和
的上方和下方,并且与圆柱面和![]() 均相切.给出下列三个结论:
均相切.给出下列三个结论:
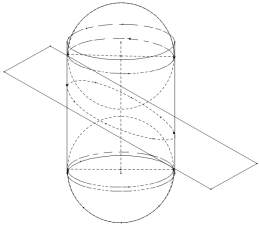
①两个球与![]() 的切点是所得椭圆的两个焦点;
的切点是所得椭圆的两个焦点;
②若球心距![]() ,球的半径为
,球的半径为![]() ,则所得椭圆的焦距为2;
,则所得椭圆的焦距为2;
③当圆柱的轴与![]() 所成的角由小变大时,所得椭圆的离心率也由小变大.
所成的角由小变大时,所得椭圆的离心率也由小变大.
其中,所有正确结论的序号是( )
A.①B.②③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数m,使得
,若存在实数m,使得![]() 为R上的奇函数,则称
为R上的奇函数,则称![]() 是位差值为m的“位差奇函数”.
是位差值为m的“位差奇函数”.
(1)判断函数![]() 和
和![]() 是否是位差奇函数,并说明理由;
是否是位差奇函数,并说明理由;
(2)若![]() 是位差值为
是位差值为![]() 的位差奇函数,求
的位差奇函数,求![]() 的值;
的值;
(3)若对于任意![]() ,
,![]() 都不是位差值为m的位差奇函数,求实数t的取值范围.
都不是位差值为m的位差奇函数,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 是函数
是函数![]() 的反函数,解方程
的反函数,解方程![]() ;
;
(2)当![]()
![]() 时,定义
时,定义![]() ,设
,设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() 及
及![]() ;
;
(3)对于任意![]() ,其中
,其中![]() ,当
,当![]() 能作为一个三角形的三边长时,
能作为一个三角形的三边长时,![]() 也总能作为一个三角形的三边长,试探究M的最小值.
也总能作为一个三角形的三边长,试探究M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与直线
与直线![]() 有且只有一个交点,点P为椭圆C上任一点,
有且只有一个交点,点P为椭圆C上任一点,![]() ,
,![]() .若
.若![]() 的最小值为
的最小值为![]() .
.
(1)求椭圆C的标准方程;
(2)设直线![]() 与椭圆C交于不同两点A,B,点O为坐标原点,且
与椭圆C交于不同两点A,B,点O为坐标原点,且![]() ,当
,当![]() 的面积S最大时,求
的面积S最大时,求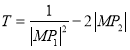 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com