
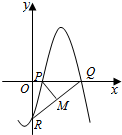
 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )| A. | 2$\sqrt{3}$ | B. | $\frac{7\sqrt{3}}{3}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | 4$\sqrt{3}$ |
分析 由题意设出Q(2a,0)a>0,R(0,b),b<0,求出a,b的值,通过五点法求出函数的解析式,即可求出A.
解答 解:∵函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0)、M(2,-2)为线段QR的中点,
∴设Q(2a,0),a>0,R(0,b),b<0,
则$\left\{\begin{array}{l}{\frac{2a+0}{2}=2}\\{\frac{0+b}{2}=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=-4}\end{array}\right.$,
即Q(4,0),R(0,-4),
则函数的周期T=2×(4-1)=6,
即$\frac{2π}{ω}=6$,即ω=$\frac{π}{3}$,
则f(x)=Asin($\frac{π}{3}$x+φ),
∵f(1)=0,且f(0)=-4,
∴Asin($\frac{π}{3}$+φ)=0,且Asinφ=-4,
即$\frac{π}{3}$+φ=kπ,k∈Z,
则φ=kπ-$\frac{π}{3}$,
∵φ|≤$\frac{π}{2}$,
∴当k=0时,φ=-$\frac{π}{3}$,
则Asin(-$\frac{π}{3}$)=-4,
即$-\frac{\sqrt{3}}{2}$A=-4,
解得A=$\frac{8}{\sqrt{3}}$=$\frac{8\sqrt{3}}{3}$,
故选:C
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得Q点与R点的坐标是关键,考查识图、运算与求解能力,属于中档题.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
 如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,
如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 结论正确 | D. | 推理形式错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | 6π | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{15}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (-∞,4] | C. | (4,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|\overrightarrow a|=\sqrt{x_1^2+y_1^2}$ | B. | $\overrightarrow a•\overrightarrow b={x_1}{x_2}+{y_1}{y_2}$ | ||
| C. | $\overrightarrow a⊥\overrightarrow b?{x_1}{x_2}+{y_1}{y_2}=0$ | D. | $\overrightarrow a∥\overrightarrow b={x_1}{y_2}+{x_2}{y_1}=0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com