
分析 (Ⅰ)由题意可知,2c=2$\sqrt{3}$,2a=4,b2=a2-c2,即可求得a和b的值,写出椭圆的方程;
(Ⅱ)将直线方程代入椭圆方程,求得关于x的一元二次方程,利用根与系数的关系求得x1+x2和x1•x2,并代入直线方程求得y1•y2,表示出$\overrightarrow{AP}$和$\overrightarrow{AQ}$,利用向量数量积的坐标表示求得$\overrightarrow{AP}$•$\overrightarrow{AQ}$>0,因此点A在⊙M外.
解答 解:(Ⅰ)依题意得,2c=2$\sqrt{3}$,2a=4,即c=$\sqrt{3}$,a=$\sqrt{3}$,(2分)
∴b2=a2-c2=1,(3分)
所以E的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.(4分)
(Ⅱ)点A在⊙M外.理由如下:(5分)
设P(x1,y1),Q(x2,y2),
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$得(1+4k2)x2-8k2x+4k2-4=0,(6分)
所以,△=(-8k2)2-4(1+4k2)(4k2-4)=48k2+16>0,
所以x1+x2=$\frac{8{k}^{2}}{1+4{k}^{2}}$,x1•x2=$\frac{4{k}^{2}-4}{1+4{k}^{2}}$.(8分)
因为$\overrightarrow{AP}$=(x1-2,y1),$\overrightarrow{AQ}$=(x2-2,y2),
所以$\overrightarrow{AP}$•$\overrightarrow{AQ}$=(x1-2)(x2-2)+y1•y2,
=(1+k2)x1•x2-(2+k2)(x1+x2)+4+k2,
=$\frac{4({k}^{2}+1)({k}^{2}-1)}{1+4{k}^{2}}$-$\frac{8{k}^{2}(2+{k}^{2})}{1+4{k}^{2}}$+4+k2,(10分)
=$\frac{{k}^{2}}{1+4{k}^{2}}$.
因为k≠0,
所以$\overrightarrow{AP}$•$\overrightarrow{AQ}$>0.
∴cos∠PAQ>0,
∴∠PAQ为锐角,
所以点A在⊙M外.(12分)
点评 本题考查椭圆的标准方程及椭圆的基本性质,点与圆、直线与椭圆的位置关系等基础知识,考查运算求解能力、推理论证能力、化归与转化思想等,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有95%以上的把握认为“吸烟与患肺病有关” | |
| B. | 有95%以上的把握认为“吸烟与患肺病无关” | |
| C. | 有99%以上的把握认为“吸烟与患肺病有关” | |
| D. | 有99%以上的把握认为“吸烟与患肺病无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
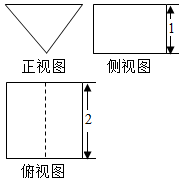 一个多面体的三视图如图所示,正视图为等腰直角三角形,俯视图中虚线平分矩形的面积,则该多面体的表面积为( )
一个多面体的三视图如图所示,正视图为等腰直角三角形,俯视图中虚线平分矩形的面积,则该多面体的表面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com