
分析 (1)由已知得直线l:$\frac{x}{a}+\frac{y}{b}$=1,再由由d=r,能求出a,b满足的条件.
(2)由a,b满足的条件得到ab+2=2(a+b)$≥2•2\sqrt{ab}$,由此能求出△AOB的面积最小值.
解答 解:(1)∵与曲线C:x2+y2-2x-2y+1=0相切的直线l与x轴、y轴的正半轴交于两点A,B,
又O为原点,|OA|=a,|OB|=b,a>2,b>2,
∴直线l:$\frac{x}{a}+\frac{y}{b}$=1,
由d=r,知$\frac{|b+a-ab|}{\sqrt{{a}^{2}+{b}^{2}}}=1$,
整理得a,b满足的条件为:2-2a-2b+ab=0. (6分)
(2)∵2-2a-2b+ab=0,
∴ab+2=2(a+b)$≥2•2\sqrt{ab}$,
解得$\sqrt{ab}≤2-\sqrt{2}$或$\sqrt{ab}$≥2+$\sqrt{2}$,
又a>2,b>2,∴ab≥6+4$\sqrt{2}$,∴${S}_{△AOB}≥\frac{1}{2}ab=3+2\sqrt{2}$,
∴△AOB的面积最小值为3+2$\sqrt{2}$,此时a=b=2+$\sqrt{2}$.(12分)
点评 本题考查a,b满足的条件和△AOB面积的最小值的求法,是中档题,解题时要注意直线方程、圆的性质、点到直线的距离、均值定理等知识点的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
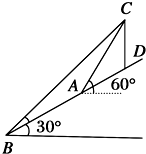 如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为48m,斜坡与水平面成30°角,则铁塔CD的高为16$\sqrt{3}$m.
如图,要在山坡上A、B两处测量与地面垂直的铁塔CD的高,由A、B两处测得塔顶C的仰角分别为60°和45°,AB长为48m,斜坡与水平面成30°角,则铁塔CD的高为16$\sqrt{3}$m.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com