
 表示取出的2个小球上的数字之和,求随机变量
表示取出的2个小球上的数字之和,求随机变量 的概率分布与数学期望.
的概率分布与数学期望. 、(Ⅱ)
、(Ⅱ)
 ,∵从袋中的6个小球中任取2个小球的方法共有
,∵从袋中的6个小球中任取2个小球的方法共有 种,其中取出的2个小球上的数字互不相同的方法有
种,其中取出的2个小球上的数字互不相同的方法有 ,
, .-------6分
.-------6分 ,“取出的2个小球上的数字相同”的事件记为
,“取出的2个小球上的数字相同”的事件记为 ,则事件
,则事件 与事件
与事件 是对立事件.∵
是对立事件.∵ ,
, .------6分
.------6分 所有可能的取值为:2,3,4,5,6.
所有可能的取值为:2,3,4,5,6.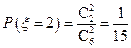 ,
, ,
, ,
,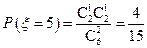 ,
, .
. 的概率分布为:
的概率分布为: | 2 | 3 | 4 | 5 | 6 |
 | 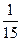 | 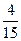 |  | 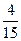 | 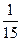 |
 的数学期望
的数学期望 .---13分
.---13分

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ;乙抛掷3次,记正面朝上的次为
;乙抛掷3次,记正面朝上的次为 .(Ⅰ)分别求
.(Ⅰ)分别求 和
和 的期望;(Ⅱ)规定:若
的期望;(Ⅱ)规定:若 >
> ,则甲获胜;否则,乙获胜.求甲获胜的概率.
,则甲获胜;否则,乙获胜.求甲获胜的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 服从以下分布:
服从以下分布: | 10 | 20 | 30 | 40 | 50 |
 | 0.15 | 0.20 | 0.25 | 0.30 | 0.10 |
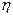 服从二项分布
服从二项分布 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的概率分布列与期望.
的概率分布列与期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com