
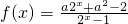 (x∈R,x≠0),其中a为常数,且a<0.
(x∈R,x≠0),其中a为常数,且a<0.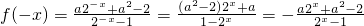 (2分)
(2分)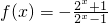 ,
,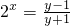 ,∴
,∴ (6分)
(6分)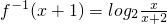 (x>0或x<-2)(7分)
(x>0或x<-2)(7分)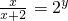 可得:
可得: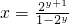 ,
,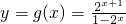 (9分)
(9分) (11分)
(11分)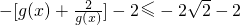 即
即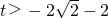 (12分)
(12分) (13分)
(13分)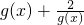 在g(x)∈(-∞,-2)单调递增,
在g(x)∈(-∞,-2)单调递增,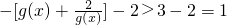 即t≤1(15分)
即t≤1(15分) (16分)
(16分)

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
| ln(x+n)-n |
| x+n |
| 1 |
| n(n+1) |
| x |
| ex-1 |
| 1 |
| en+1+e•n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:天利38套《2008全国各省市高考模拟试题汇编(大纲版)》、数学文 大纲版 题型:044
已知函数f(x)=x3+bx2+cx+d(b、c、d∈R且都为常数)的导函数为![]() ,且f(1)=7,设F(x)=f(x)-ax2(a∈R).
,且f(1)=7,设F(x)=f(x)-ax2(a∈R).
(Ⅰ)当a<2时,求F(x)的极小值;
(Ⅱ)若对任意的x∈[0,+∞),都有F(x)≥0成立,求a的取值范围并证明不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源:新疆兵团二中2012届高三第六次月考数学理科试题 题型:044
已知函数f(x)=Asin(ωx+![]() )(x∈R,A>0,ω>0,0<
)(x∈R,A>0,ω>0,0<![]() <
<![]() )图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|
)图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|![]() |=2,|
|=2,|![]() |=
|=![]() ,|
,|![]() |=
|=![]() .
.

(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)图象向右平移1个单位后得到函数y=g(x)的图象,当x∈[0,2]时,求函数h(x)=f(x)·g(x)的最大值.
查看答案和解析>>
科目:高中数学 来源:新疆兵团二中2012届高三第六次月考数学文科试题 题型:044
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<![]() )图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|
)图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|![]() |=2,|
|=2,|![]() |=
|=![]() ,|
,|![]() |=
|=![]() .
.

(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)图象向右平移1个单位后得到函数y=g(x)的图象,当x∈[0,2]时,求函数h(x)=f(x)·g(x)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com