
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为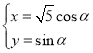 (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 、
、![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() 与曲线
与曲线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() (且点
(且点![]() ,
,![]() 均异于原点
均异于原点![]() ),当
),当![]() 时,求
时,求![]() 的最小值.
的最小值.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,△PAC为等腰直角三角形,![]() 为正三角形,D为A的中点,AC=2.
为正三角形,D为A的中点,AC=2.
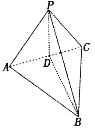
(1)证明:PB⊥AC;
(2)若三棱锥![]() 的体积为
的体积为![]() ,求二面角A—PC—B的余弦值
,求二面角A—PC—B的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足:
满足:![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() .
.
① 记![]() ,求证:数列
,求证:数列![]() 为等差数列;
为等差数列;
② 若数列![]() 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项![]() 应满足的条件.
应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节来临之际,某超市为了确定此次春节年货的进货方案,统计去年春节前后50天年货的日销售量(单位:kg),得到如图所示的频率分布直方图.
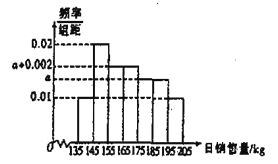
(1)求这50天超市日销售量![]() 的平均数;(视频率为概率,以各组区间的中点值代表该组的值)
的平均数;(视频率为概率,以各组区间的中点值代表该组的值)
(2)先从日销售在![]() ,
,![]() ,
,![]() 内的天数中,按分层抽样随机抽取4天进行比较研究,再从中选2天,求这2天的日销售量都在
内的天数中,按分层抽样随机抽取4天进行比较研究,再从中选2天,求这2天的日销售量都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() :
:![]()
![]() 的左、右焦点,且椭圆
的左、右焦点,且椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值为
的距离的最小值为![]() .点M、N是椭圆
.点M、N是椭圆![]() 上位于
上位于![]() 轴上方的两点,且向量
轴上方的两点,且向量![]() 与向量
与向量![]() 平行.
平行.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 时,求△
时,求△![]() 的面积;
的面积;
(3)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对于任意
,对于任意![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,其前
,其前![]() 项和为
项和为![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:对于任意正整数
,求证:对于任意正整数![]() ,都有
,都有![]() ;
;
(3)将数列![]() 、
、![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面”,“当
放在前面”,“当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行“交叉排列”得到一个新的数列:
放在前面”的要求进行“交叉排列”得到一个新的数列:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 求这个新数列的前
求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,在(Ⅰ)的条件下,试判断
,在(Ⅰ)的条件下,试判断![]() 在
在![]() 上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华东师大二附中乐东黄流中学位于我国南海边,有一片美丽的沙滩和一弯天然的海滨浴场.如图,海岸线MAN,![]() ,
,![]() (海岸线MAN上方是大海),现用长为BC的栏网围成一个三角形学生游泳场所,其中
(海岸线MAN上方是大海),现用长为BC的栏网围成一个三角形学生游泳场所,其中![]() .
.
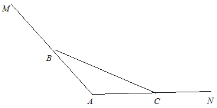
(1)若![]() ,求三角形游泳场所面积最大值;
,求三角形游泳场所面积最大值;
(2)若BC=600,![]() ,由于学生人数的增加需要扩大游泳场所面积,现在折线MBCN上方选点D,现用长为BD,DC的栏围成一个四边形游泳场所DBAC,使
,由于学生人数的增加需要扩大游泳场所面积,现在折线MBCN上方选点D,现用长为BD,DC的栏围成一个四边形游泳场所DBAC,使![]() ,求四边形游泳场所DBAC的最大面积.
,求四边形游泳场所DBAC的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com