
【题目】已知函数![]() .
.
(1)求定义域,并判断函数f(x)的奇偶性;
(2)若f(1)+f(2)=0,证明函数f(x)在(0,+∞)上的单调性,并求函数f(x)在区间[1,4]上的最值.
【答案】(1)![]() ,奇函数 (2)单调递增,证明见详解,最大值
,奇函数 (2)单调递增,证明见详解,最大值![]() ,最小值-1;
,最小值-1;
【解析】
(1)由题意可得,x≠0,然后检验f(-x)与f(x)的关系即可判断;
(2)由f(1)+f(2)=a-2+2a-1=0,代入可求a,然后结合单调性的定义即可判断单调性,再由单调性可求函数f(x)在区间[1,4]上的最大值f(4),最小值f(1).即可求解.
(1)由题意可得,x≠0,故定义域为![]()
∵f(-x)=-ax+![]() =-f(x),
=-f(x),
∴f(x)为奇函数;
(2)由f(1)+f(2)=a-2+2a-1=0,
∴a=1,f(x)=x-![]() ,
,
设0<x1<x2,
则f(x1)-f(x2)=x1-x2![]() =(x1-x2)(1+
=(x1-x2)(1+![]() ),
),
∵0<x1<x2,
∴x1-x2<0,1+![]() >0,
>0,
∴(x1-x2)(1+![]() )<0,即f(x1)<f(x2),
)<0,即f(x1)<f(x2),
∴f(x)在(0,+∞)上的单调递增,
∴函数f(x)在区间[1,4]上的最大值为f(4)=![]() ,最小值为f(1)=-1.
,最小值为f(1)=-1.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】光对物体的照度与光的强度成正比,比例系数为![]() ,与光源距离的平方成反比,比例系数为
,与光源距离的平方成反比,比例系数为![]() 均为正常数
均为正常数![]() 如图,强度分别为8,1的两个光源A,B之间的距离为10,物体P在连结两光源的线段AB上
如图,强度分别为8,1的两个光源A,B之间的距离为10,物体P在连结两光源的线段AB上![]() 不含A,
不含A,![]() 若物体P到光源A的距离为x.
若物体P到光源A的距离为x.
![]()
![]() 试将物体P受到A,B两光源的总照度y表示为x的函数,并指明其定义域;
试将物体P受到A,B两光源的总照度y表示为x的函数,并指明其定义域;
![]() 当物体P在线段AB上何处时,可使物体P受到A,B两光源的总照度最小?
当物体P在线段AB上何处时,可使物体P受到A,B两光源的总照度最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为正方形,侧棱
中,底面ABCD为正方形,侧棱![]() 底面ABCD,且
底面ABCD,且![]() ,E,F,H分别是线段PA,PD,AB的中点.
,E,F,H分别是线段PA,PD,AB的中点.
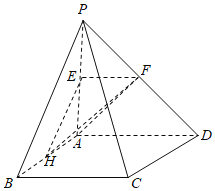
(1)求证:![]() 平面EFH;
平面EFH;
(2)求证:![]() 平面AHF;
平面AHF;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 且与
且与![]() 轴不重合的直线
轴不重合的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过点
为直径的圆过点![]() .
.
(ⅰ)求![]() 的方程;
的方程;
(ⅱ)记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商销售某种产品,在一个销售季度内,每售出![]() 该产品获利润
该产品获利润![]() 元;未售出的产品,每
元;未售出的产品,每![]() 亏损
亏损![]() 元.根据以往的销售记录,得到一个销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了
元.根据以往的销售记录,得到一个销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了![]() 该产品.用
该产品.用![]() (单位:
(单位:![]() ,
,![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,![]() (单位:元)表示下一个销售季度内经销该产品的利润.
(单位:元)表示下一个销售季度内经销该产品的利润.

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据直方图估计利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,对任意实数x,y满足f(x+y)=f(x)+f(y)+![]() ,且f(
,且f(![]() )=0,当x>
)=0,当x>![]() 时,f(x)>0.给出以下结论
时,f(x)>0.给出以下结论
①f(0)=-![]()
②f(-1)=-![]()
③f(x)为R上减函数
④f(x)+![]() 为奇函数;
为奇函数;
⑤f(x)+1为偶函数
其中正确结论的有( )个
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于曲线![]() ,给出下列四个结论:①曲线
,给出下列四个结论:①曲线![]() 是椭圆;②关于坐标原点中心对称;③关于直线
是椭圆;②关于坐标原点中心对称;③关于直线![]() 轴对称;④所围成封闭图形面积小于8.则其中正确结论的序号是( )
轴对称;④所围成封闭图形面积小于8.则其中正确结论的序号是( )
A. ②④ B. ②③④ C. ①②③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com