
【题目】设![]() 是
是![]() 在点
在点![]() 处的切线.
处的切线.
(1)求证: ![]() ;
;
(2)设![]() ,其中
,其中![]() .若
.若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)求导得切线斜率,进而得切线方程,令![]() ,求导利用单调性可得
,求导利用单调性可得![]() ,从而得证.
,从而得证.
(2)由![]() ,结合定义域
,结合定义域![]() ,讨论
,讨论![]() 时,由
时,由![]() 可得
可得![]() ,得函数单增,可证得,讨论
,得函数单增,可证得,讨论![]() 时,由导数可得存在
时,由导数可得存在![]() ,使得
,使得![]() ,
,![]() ,从而得解.
,从而得解.
(1)设![]() ,则
,则![]() ,所以
,所以![]() .所以
.所以![]() .
.
令![]() .
.
![]() 满足
满足![]() ,且
,且![]() .
.
当![]() 时,
时,![]() ,故
,故![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,故
,故![]() 单调递增.
单调递增.
所以,![]() .所以
.所以![]() .
.
(2)法一:![]() 的定义域是
的定义域是![]() ,且
,且![]() .
.
① 当![]() 时,由(1)得
时,由(1)得![]() ,
,
所以![]() .
.
所以 ![]() 在区间
在区间![]() 上单调递增, 所以
上单调递增, 所以![]() 恒成立,符合题意.
恒成立,符合题意.
② 当![]() 时,由
时,由![]() ,且
,且![]() 的导数
的导数![]() ,
,
所以 ![]() 在区间
在区间![]() 上单调递增.
上单调递增.
因为![]() ,
,
于是存在![]() ,使得
,使得![]() .
.
所以 ![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]() ,此时
,此时![]() 不会恒成立,不符合题意.
不会恒成立,不符合题意.
综上, ![]() 的取值范围是
的取值范围是![]() .
.
法二:∵![]()
∴![]()
当![]()
当![]()
令![]() =
=![]()
令![]() ,
,![]()
![]()
故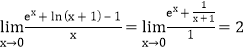 ,故
,故![]() ,
,
综上![]() .
.


科目:高中数学 来源: 题型:
【题目】一袋中装有6个黑球,4个白球.如果不放回地依次取出2个球.求:
(1)第1次取到黑球的概率;
(2)第1次和第2次都取到黑球的概率;
(3)在第1次取到黑球的条件下,第2次又取到黑球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),圆
为参数),圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 分别与圆
分别与圆![]() 和圆
和圆![]() 交于不同于原点的点
交于不同于原点的点![]() 和
和![]() .
.
(1)以直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,求圆
轴的正半轴为极轴,建立极坐标系,求圆![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1(a>b>0)的中心在原点,焦点在x轴上,焦距为2,且与椭圆x2+
=1(a>b>0)的中心在原点,焦点在x轴上,焦距为2,且与椭圆x2+ ![]() =1有相同离心率,直线l:y=kx+m与椭圆C交于不同的A,B两点.
=1有相同离心率,直线l:y=kx+m与椭圆C交于不同的A,B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足 ![]() ,(O为坐标原点),求实数λ取值范围.
,(O为坐标原点),求实数λ取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6 ![]() ,则BC的长为 .
,则BC的长为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某测试中,卷面满分为100分,60分为及格,为了调查午休对本次测试前两个月复习效果的影响,特对复习中进行午休和不进行午休的考生进行了测试成绩的统计,数据如下表所示:
分数段 | 29~ 40 | 41~ 50 | 51~ 60 | 61~ 70 | 71~ 80 | 81~ 90 | 91~ 100 |
午休考 生人数 | 23 | 47 | 30 | 21 | 14 | 31 | 14 |
不午休 考生人数 | 17 | 51 | 67 | 15 | 30 | 17 | 3 |
(1)根据上述表格完成列联表:
及格人数 | 不及格人数 | 总计 | |
午休 | |||
不午休 | |||
总计 |
(2)根据列联表可以得出什么样的结论?对今后的复习有什么指导意义?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生寒假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表:
本数 | 0 | 1 | 2 | 3 | 4 | 5 |
男生 | 0 | 1 | 4 | 3 | 2 | 2 |
女生 | 0 | 0 | 1 | 3 | 3 | 1 |
(I)从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为4的概率;
(II)若从阅读名著不少于4本的学生中任选4人,设选到的男学生人数为 X,求随机变量 X的分布列和数学期望;
(III)试判断男学生阅读名著本数的方差 ![]() 与女学生阅读名著本数的方差
与女学生阅读名著本数的方差 ![]() 的大小(只需写出结论).
的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在斜三棱柱ABC﹣A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.
(I)证明:BC1∥平面 A1EC;
(II)若A1A⊥A1B,且AB=2.
①求点B到平面ACC1A1的距离;
②求直线CB1与平面ACC1A1所成角的正弦值.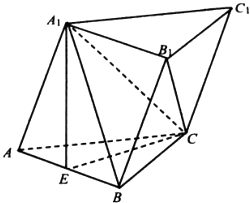
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在x轴的椭圆的离心率与双曲线3x2-y2=3的离心率互为倒数,且过点![]() ,求:(1)求椭圆方程;
,求:(1)求椭圆方程;
(2)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M,N,点![]() ,有|MP|=|NP|,求k的取值范围.
,有|MP|=|NP|,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com