
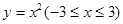 绕
绕 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是 .
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是 . 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源:不详 题型:解答题
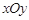 中,以坐标原点
中,以坐标原点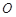 为极点,
为极点,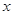 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线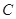 的极坐标方程为
的极坐标方程为 ,直线
,直线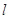 的参数方程为
的参数方程为 为参数,
为参数,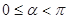 ).
).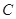 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;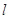 经过点
经过点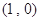 ,求直线
,求直线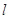 被曲线
被曲线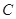 截得的线段
截得的线段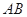 的长.
的长.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
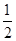 .
. ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
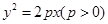 的焦点为F,过抛物线上点
的焦点为F,过抛物线上点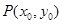 的切线为
的切线为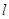 ,过P点作平行于x轴的直线m,过焦点F作平行于
,过P点作平行于x轴的直线m,过焦点F作平行于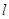 的直线交m于M,则
的直线交m于M,则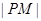 的长为( )
的长为( )A.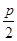 | B.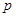 | C.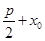 | D.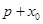 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com