证明:(1)条件的必要性是显然的,
因为已知a>0,b>0,c>0,
所以立即可得a+b+c>0,
ab+bc+ca>0,abc>0.
下面证明条件的充分性:
设a,b,c是三次方程x
3+px
2+qx+r=0的三个根,
则由根与系数的关系及已知条件有-p=a+b+c>0,
q=ab+bc+ca>0,-r=abc>0,
此即p<0,q>0,r<0.
由此即可知三次方程x
3+px
2+qx+r=0的系数正负相间,
所以此方程无负根,即方程根均非负;
又由abc>0可知,方程无零根,
故a>0,b>0,c>0;
(2)由(1)的证明可知,α,β,γ均为正数的充要条件是p<0,q>0,r<0.
于是问题转化为证明α,β,γ为三角形三条边的充要条件为p
3>4pq-8r
条件的必要性:
若α,β,γ为三角形的三边,
则由三角形的性质必有α+β>γ,β+γ>α,γ+α>β.
于是α+β-γ>0,β+γ-α>0,γ+α-β>0.
由此可得(α+β-γ)(β+γ-α)(γ+α-β)
=(-p-2α)(-p-2β)(-p-2γ)
=-(p+2α)(p+2β)(p+2γ)
=-[p
3+2(α+β+γ)p
2+4(βγ+γα+αβ)p+8αβγ]
=-(p
3-2p
3+4pq-8r)=p
3-4pq+8r>0
即p
3>4pq-8r.
条件的充分性:若p
3>4pq-8r,
则p
3-4pq+8r>0,
-(α+β+γ)
3+4(α+β+γ)(αβ+βγ+γα)-8αβγ>0,
(α+β+γ)(2αβ+2βγ+2γα-α
2-β
2-γ
2)-8αβγ>0,
[α+(β+γ)][-(β-γ)
2+2α(β+γ)-α
2]-8αβγ>0,
-α
3+α
2(β+γ)+α(β-γ)
2-(β+γ)(β-γ)
2>0,
α
2(-α+β+γ)+(β-γ)
2(α-β-γ)>0,
(-α+β+γ)[α
2-(β-γ)
2]>0,
(-α+β+γ)(α+β-γ)(α-β+γ)>0.
此式中至少有一因式大于0,今设-α+β+γ>0,
则必有(α+β-γ)(α-β+γ)>0.
如果α+β-γ<0,α-β+γ<0,
两式相加得2a<0,
即α<0,此与α>0相矛盾
故有-α+β+γ>0,α+β-γ>0,α-β+γ>0,
此即

此即α,β,γ可作为一个三角形的三条边.
综上所证可知,
方程x
3+px
2+qx+r=0的三根α,β,γ为一个三角形的三条边的充要条件是
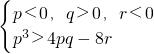
.
分析:(1)必要性显然,关键是证明充分性.可设a,b,c是三次方程x
3+px
2+qx+r=0的三个根,利用根与系数的关系及已知条件即可证明a,b,c满足的条件,从而得出a,b,c是整数.
(2)借助(1)的证明,问题转化为证明α,β,γ为三角形三条边的充要条件为p
3>4pq-8r.由三角形的性质和适当的计算,即可证明此充要条件.
点评:此题考查必要条件、充分条件与充要条件的判别,同时考查三次方程根的相关知识以及三角形边的性质.

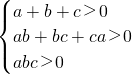 ;
;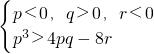 .
.
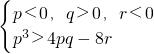 .
.

 名校课堂系列答案
名校课堂系列答案