
【题目】设函数![]() ,若函数
,若函数![]() 在
在![]() 内有两个极值点,则实数
内有两个极值点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B. (0,1)
B. (0,1)
C. (0,2) D. ![]()
【答案】B
【解析】
函数![]() 在
在![]() 内有两个极值点,即
内有两个极值点,即![]() 在
在![]() 有两个零点,可转化为函数
有两个零点,可转化为函数![]() 与函数
与函数![]() 在区间
在区间![]() 上有两个交点,通过数形结合可以求出答案。
上有两个交点,通过数形结合可以求出答案。
对函数![]() 求导,可得
求导,可得![]() ,
,
由题意可知,函数![]() 与函数
与函数![]() 在区间
在区间![]() 上有两个交点,
上有两个交点,
对函数![]() 求导,
求导,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
且当![]() 时,
时,![]() ,结合单调性可以画出函数
,结合单调性可以画出函数![]() 在
在![]() 大致图象(如下图)。
大致图象(如下图)。
函数![]() 是斜率为
是斜率为![]() 且恒过点(1,0)的直线,设
且恒过点(1,0)的直线,设![]() 与
与![]() 相切时直线斜率为
相切时直线斜率为![]() ,
,
则当![]() 时,函数
时,函数![]() 与函数
与函数![]() 在区间
在区间![]() 上有两个交点,
上有两个交点,
设切点为(![]() ),则
),则![]() ,
,![]() ,
,
则切线方程为![]() ,
,
因为切线过点(1,0),则![]() ,
,
解得![]() 或
或![]() ,
,
因为![]() ,所以只有
,所以只有![]() 满足题意,
满足题意,
此时切线方程为![]() ,
,![]() ,
,
所以当![]() 时,函数
时,函数![]() 与函数
与函数![]() 在区间
在区间![]() 上有两个交点,即函数
上有两个交点,即函数![]() 在
在![]() 内有两个极值点。
内有两个极值点。
故选B.


科目:高中数学 来源: 题型:
【题目】![]() 是定义在
是定义在![]() 上且满足如下条件的函数
上且满足如下条件的函数![]() 组成的集合:①对任意的
组成的集合:①对任意的![]() ,都有
,都有![]() ②存在常数
②存在常数![]() 使得对任意的
使得对任意的![]() ,都有
,都有![]() .
.
(1)设![]() 问
问![]() 是否属于
是否属于![]() ?说明理由;
?说明理由;
(2)若![]() 如果存在
如果存在![]() 使得
使得![]() 证明:这样的
证明:这样的![]() 是唯一的;
是唯一的;
(3)设![]() 且
且![]() 试求
试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对某校高二文科学生的记忆力x和判断力y进行统计分析,得下表数据.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
参考公式: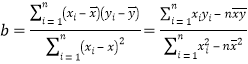
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
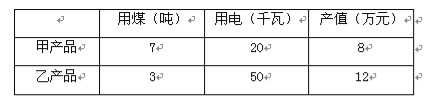
但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量, ![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
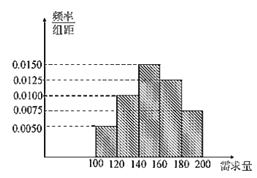
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数;
的平均数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于4000元的概率.
不少于4000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com