
【题目】若函数f(x)= ![]() sin2x+2cos2x+m在区间[0,
sin2x+2cos2x+m在区间[0, ![]() ]上的最大值为6,求常数m的值及此函数当x∈R时的最小值,并求相应的x的取值集合.
]上的最大值为6,求常数m的值及此函数当x∈R时的最小值,并求相应的x的取值集合.
【答案】解:f(x)= ![]() sin2x+2cos2x+m
sin2x+2cos2x+m
= ![]() sin2x+1+cos2x+m
sin2x+1+cos2x+m
=2sin(2x+ ![]() )+m+1,
)+m+1,
∵x ![]() ,∴2x+
,∴2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],![]() sin(2x+
sin(2x+ ![]() )≤1,
)≤1,
所以函数f(x)的最大值为3+m,
∴3+m=6,m=3,
∴f(x)=2sin(2x+ ![]() )+4,
)+4,
当x∈R时,函数f(x)的最小值为2,
此时2x+ ![]() =﹣
=﹣ ![]() ,
,
即x=﹣ ![]() +kπ(k∈Z)时取最小值.
+kπ(k∈Z)时取最小值.
【解析】先利用两角和的正弦公式化成标准形式,根据x的范围求函数的最大值,然后让最大值等于6,求出m的值;当x∈R时,根据正弦函数求函数的最小值及取到最小值时的x的值.
【考点精析】解答此题的关键在于理解二倍角的余弦公式的相关知识,掌握二倍角的余弦公式:![]() ,以及对三角函数的最值的理解,了解函数
,以及对三角函数的最值的理解,了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分8分) 已知抛物线C:y=-x2+4x-3 .
(1)求抛物线C在点A(0,-3)和点B(3,0)处的切线的交点坐标;
(2)求抛物线C与它在点A和点B处的切线所围成的图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且
上,且![]() .
.
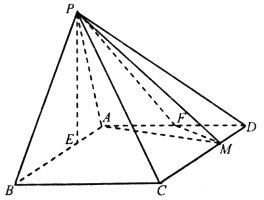
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)当平面![]() 与平面
与平面![]() 所成的二面角的正弦值为
所成的二面角的正弦值为![]() 时,求四棱锥
时,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() ,
, ![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,
, ![]() ,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】样本a1 , a2 , a3 , …,a10的平均数为 ![]() ,样本b1 , b2 , b3 , …,b10的平均数为
,样本b1 , b2 , b3 , …,b10的平均数为 ![]() ,那么样本a1 , b1 , a2 , b2 , …,a10 , b10的平均数为( )
,那么样本a1 , b1 , a2 , b2 , …,a10 , b10的平均数为( )
A.![]() +
+ ![]()
![]()
B.![]() (
( ![]() +
+ ![]() )
)![]()
C.2( ![]() +
+ ![]() )
)
D.![]() (
( ![]() +
+ ![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①函数 ![]() 是奇函数;
是奇函数;
②存在实数x,使sinx+cosx=2;
③若α,β是第一象限角且α<β,则tanα<tanβ;
④ ![]() 是函数
是函数 ![]() 的一条对称轴;
的一条对称轴;
⑤函数 ![]() 的图象关于点
的图象关于点 ![]() 成中心对称.
成中心对称.
其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】咖啡馆配制两种饮料,甲种饮料分别用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。乙种饮料分别用奶粉
。乙种饮料分别用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。已知每天使用原料限额为奶粉
。已知每天使用原料限额为奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。如果甲种饮料每杯能获利
。如果甲种饮料每杯能获利![]() 元,乙种饮料每杯能获利
元,乙种饮料每杯能获利![]() 元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某货轮匀速行驶在相距![]() 海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为
海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为![]() ),其他费用为每小时
),其他费用为每小时![]() 元,且该货轮的最大航行速度为
元,且该货轮的最大航行速度为![]() 海里/小时.
海里/小时.
(1)请将从甲地到乙地的运输成本![]() (元)表示为航行速度
(元)表示为航行速度![]() (海里/小时)的函数;
(海里/小时)的函数;
(2)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com