
【题目】某地为改善旅游环境进行景点改造.如图,将两条平行观光道l1和l2通过一段抛物线形状的栈道AB连通(道路不计宽度),l1和l2所在直线的距离为0.5(百米),对岸堤岸线l3平行于观光道且与l2相距1.5(百米)(其中A为抛物线的顶点,抛物线的对称轴垂直于l3,且交l3于M),在堤岸线l3上的E,F两处建造建筑物,其中E,F到M的距离为1(百米),且F恰在B的正对岸(即BF⊥l3).
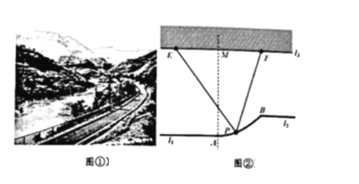
(1)在图②中建立适当的平面直角坐标系,并求栈道AB的方程;
(2)游客(视为点P)在栈道AB的何处时,观测EF的视角(∠EPF)最大?请在(1)的坐标系中,写出观测点P的坐标.
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,当点
,当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,求
为坐标原点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x24py(p为大于2的质数)的焦点为F,过点F且斜率为k(k0)的直线交C于A,B两点,线段AB的垂直平分线交y轴于点E,抛物线C在点A,B处的切线相交于点G.记四边形AEBG的面积为S.
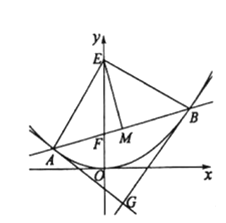
(1)求点G的轨迹方程;
(2)当点G的横坐标为整数时,S是否为整数?若是,请求出所有满足条件的S的值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]()
![]() .
.
(1)当x≥0时,f(x)≤h(x)恒成立,求a的取值范围;
(2)当x<0时,研究函数F(x)=h(x)﹣g(x)的零点个数;
(3)求证:![]() (参考数据:ln1.1≈0.0953).
(参考数据:ln1.1≈0.0953).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 和
和![]() ,右顶点为
,右顶点为![]() ,且
,且![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 作垂直
作垂直![]() 轴的直线
轴的直线![]() ,点
,点![]() 为直线
为直线![]() 上纵坐标不为零的任意一点,过
上纵坐标不为零的任意一点,过![]() 作
作![]() 的垂线交椭圆
的垂线交椭圆![]() 于点
于点![]() 和
和![]() ,当
,当![]() 时,求此时四边形
时,求此时四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() 圆台
圆台![]() 的侧面积为
的侧面积为![]() .若点
.若点![]() 分别为圆
分别为圆![]() 上的动点,且点
上的动点,且点![]() 在平面
在平面![]() 的同侧.
的同侧.

(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求多面体
的体积取最大值时,求多面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com