
形状如图所示的三个游戏盘中(图(1)是正方形,M、N分别是所在边中点,图(2)是半径分别为2和4的两个同心圆,O为圆心,图(3)是正六边形,点P为其中心)各有一个玻璃小球,依次水平摇动三个游戏盘,当小球静止后,就完成了一局游戏.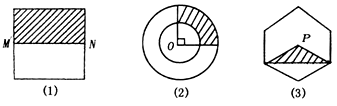
(Ⅰ)一局游戏后,这三个盘中的小球都停在阴影部分的概率是多少?
(Ⅱ)用随机变量ξ表示一局游戏后,小球停在阴影部分的事件个数与小球没有停在阴影部分的事件个数之差的绝对值,求随机变量ξ的分布列及数学期望.
(I)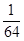 ;(II)分布列为
;(II)分布列为
∴数学期望Eξ=1×ξ 1 3 P 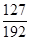
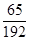
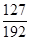 +3×
+3×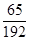 =
=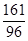 .
.
解析试题分析:(I)先根据几何概型的概率公式得到在三个图形中,小球停在阴影部分的概率,因为三个小球是否停在阴影部分相互之间没有关系,根据相互独立事件同时发生的概率得到结果.
(II)根据一次游戏结束小球停在阴影部分的事件数可能是0,1,2,3,得到ξ的可能取值是1,3,当变量等于3时,表示三个小球都在阴影部分或三个小球都不在阴影部分,这两种情况是互斥的,得到概率,分布列和期望.
试题解析:
(I)“一局游戏后,这三个盘中的小球都停在阴影部分”分别记为事件A1、A2、A3,
由题意知,A1、A2、A3互相独立,且P(A1)=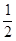 ,P(A2)=
,P(A2)=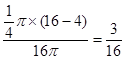 ,P(A3)=
,P(A3)=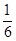 .
.
∴P(A1 A2 A3)=P(A1)P(A2) P(A3)=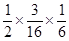 =
=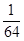 ;
;
(II)一局游戏后,这三个盘中的小球都停在阴影部分的事件数可能是0,1,2,3,相应的小球没有停在阴影部分的事件数可能取值为3,2,1,0,所以ξ可能的取值为1,3,则
P(ξ=3)=P(A1 A2 A3)+P(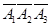 )=
)=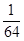 +
+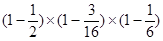 =
=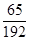
P(ξ=1)=1﹣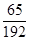 =
=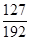
所以分布列为
∴数学期望Eξ=1×ξ 1 3 P 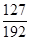
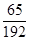
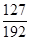 +3×
+3×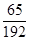 =
=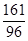 .
.
考点:1.几何概型的概率公式;2.相互独立事件同时发生的概率;3.离散型随机变量的分布列和数学期望.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:填空题
如图,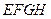 是以
是以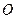 为圆心,半径为1的圆的内接正方形,将一颗豆子随机
为圆心,半径为1的圆的内接正方形,将一颗豆子随机
地扔到该圆内,用A表示事件“豆子落在正方形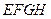 内”,B表示事件“豆子落在扇形
内”,B表示事件“豆子落在扇形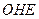 (阴影部分)内”,则(1)
(阴影部分)内”,则(1)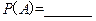 ;(2)
;(2)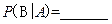

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲、乙两个盒内各任取2个球。
(1)求取出的4个球中没有红球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设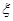 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求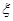 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某同学在生物研究性学习中想对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差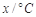 | 10 | 11 | 13 | 12 | 8 |
发芽数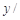 颗 颗 | 23 | 25 | 30 | 26 | 16 |
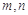 ,求事件“
,求事件“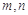 均不小于25的概率。
均不小于25的概率。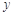 关于
关于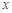 的线性回归方程
的线性回归方程 ;
;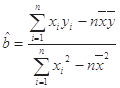 ,
,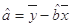 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某大学自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生两科的考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人. 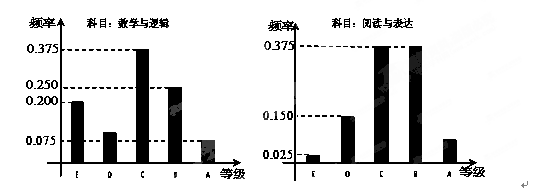
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分.
(i)求该考场考生“数学与逻辑”科目的平均分;
(ii)若该考场共有10人得分大于7分,其中有2人10分,2人9分, 6人8分. 从这10中随机抽取两人,求两人成绩之和大于等于18的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正
方形内随机投掷800个点.已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面
积是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com