
【题目】如图,从椭圆 ![]() 上一点P向x轴作垂线,垂足恰为左焦点F1 , 又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且
上一点P向x轴作垂线,垂足恰为左焦点F1 , 又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且 ![]() . (Ⅰ) 求椭圆的方程;
. (Ⅰ) 求椭圆的方程;
(Ⅱ) 若M是椭圆上的动点,点N(4,2),求线段MN中点Q的轨迹方程.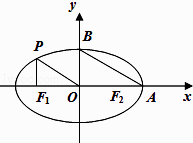
 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知p:x2﹣6x+5≤0,q:x2﹣2x+1﹣m2≤0(m>0).
(1)若m=2,且p∧q为真,求实数x的取值范围;
(2)若p是q充分不必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失. 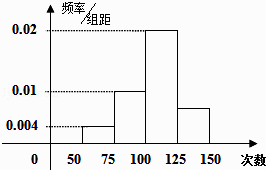
(Ⅰ) 已知第1小组频数为10,求参加这次测试的人数?
(Ⅱ) 求第4小组在y轴上的对应值;
(Ⅲ) 若次数在75次以上 ( 含75次 ) 为达标,试估计该年级跳绳测试达标率是多少?
(Ⅳ) 试估计这些数据的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点F(1,0),动点P(异于原点)在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且 ![]() ,
, ![]() .
.
(1)求动点N的轨迹C的方程;
(2)若直线l与动点N的轨迹交于A、B两点,若 ![]() 且
且 ![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2ax(a为实数),且f(1)= ![]() .
.
(1)求函数f(x)的解析式;
(2)判断函数f(x)的奇偶性并证明;
(3)判断函数f(x)在区间[0,+∞)的单调性,并用定义证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 2 | ﹣2 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一个几何体的三视图及其尺寸(单位:cm),则该几何体的表面积和体积分别为( ) 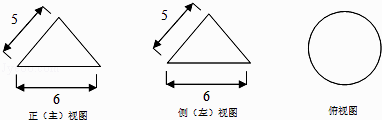
A.24πcm2 , 12πcm3
B.15πcm2 , 12πcm3
C.24πcm2 , 36πcm3
D.15πcm2 , 36πcm3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com