
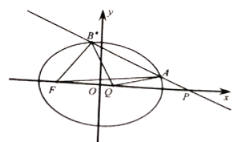
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 短轴的一个顶点到一个焦点的距离等于
短轴的一个顶点到一个焦点的距离等于![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() .
.
①若对任意直线![]() 总存在点
总存在点![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
②设点![]() 为椭圆
为椭圆![]() 的左焦点,若点
的左焦点,若点![]() 为
为![]() 的外心,求实数
的外心,求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知半圆![]() :
:![]() ,
,![]() 、
、![]() 分别为半圆
分别为半圆![]() 与
与![]() 轴的左、右交点,直线
轴的左、右交点,直线![]() 过点
过点![]() 且与
且与![]() 轴垂直,点
轴垂直,点![]() 在直线
在直线![]() 上,纵坐标为
上,纵坐标为![]() ,若在半圆
,若在半圆![]() 上存在点
上存在点![]() 使
使![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花小镇圈定一块半径为1百米的圆形荒地,准备建成各种不同鲜花景观带.为了便于游客观赏,准备修建三条道路AB,BC,CA,其中A,B,C分别为圆上的三个进出口,且A,B分别在圆心O的正东方向与正北方向上,C在圆心O南偏西某一方向上.在道路AC与BC之间修建一条直线型水渠MN种植水生观赏植物黄鸢尾(其中点M,N分别在BC和CA上,且M在圆心O的正西方向上,N在圆心O的正南方向上),并在区域MNC内种植柳叶马鞭草.
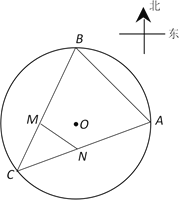
(1)求水渠MN长度的最小值;
(2)求种植柳叶马鞭草区域MNC面积的最大值(水渠宽度忽略不计).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,底面是边长为4的正三角形,
中,底面是边长为4的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
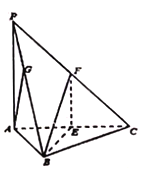
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】火把节是彝族、白族、纳西族、基诺族、拉祜族等民族的古老传统节日,有着深厚的民俗文化内涵,被称为“东方的狂欢节”凉山州旅游局为了解民众对火把节知识的知晓情况,对西昌市区 A,B 两小区的部分居民开展了问卷调查,他们得分(满分100分)数据,统计结果如下:
A小区 | ||||
得分范围/分 |
|
|
|
|
频率 |
|
|
|
|
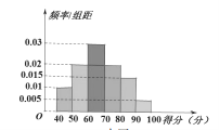
B小区
(1)以每组数据的中点值作为该组数据的代表,求B小区的平均分;
(2)若A小区得分在![]() 内的人数为
内的人数为![]() 人,B小区得分在
人,B小区得分在![]() 内的人数为
内的人数为![]() 人,求在 A,B 两小区中所有参加问卷调查的居民中得分不低于
人,求在 A,B 两小区中所有参加问卷调查的居民中得分不低于![]() 分的频率;
分的频率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为y=(-a-1)x +a-2.
(1)求直线过定点A的坐标;
(2)若l在两坐标轴上的截距相等,求l的方程;
(3)若l不经过第二象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2018年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示
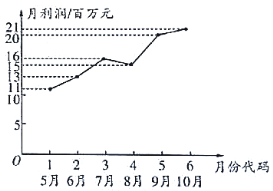
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2019年3月份的利润;
的线性回归方程,并预测该公司2019年3月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有![]() ,
,![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用
两种型号的新型材料可供选择,按规定每种新型材料最多可使用![]() 个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对
个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对![]() ,
,![]() 两种型号的新型材料对应的产品各
两种型号的新型材料对应的产品各![]() 件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .参考公式:回归直线方程为
.参考公式:回归直线方程为![]() ,其中
,其中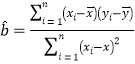
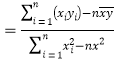 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)+![]() (ω≥0,|φ|<π)的图象与直线y=c(
(ω≥0,|φ|<π)的图象与直线y=c(![]() <c<
<c<![]() )的三个相邻交点的横坐标为2,6,18,若a=f(lg
)的三个相邻交点的横坐标为2,6,18,若a=f(lg![]() ),b=f(lg2),则以下关系式正确的是( )
),b=f(lg2),则以下关系式正确的是( )
A. a+b=0B. a﹣b=0C. a+b=1D. a﹣b=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果有穷数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() 为正整数)满足条件
为正整数)满足条件![]() 、
、![]() 、
、![]() ,即
,即![]() ,我们称其为“对称数列”.例如,数列
,我们称其为“对称数列”.例如,数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 与数列
与数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 都是“对称数列”.
都是“对称数列”.
(1)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 、
、![]() 、
、![]() 、
、![]() 是等差数列,且
是等差数列,且![]() ,
,![]() ,依次写出
,依次写出![]() 的每一项;
的每一项;
(2)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 、
、![]() 、
、![]() 、
、![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,求
的等比数列,求![]() 各项的和
各项的和![]() ;
;
(3)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 、
、![]() 、
、![]() 、
、![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,求
的等差数列,求![]() 前
前![]() 项的和
项的和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com