
已知函数f(x)=lg(x+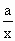 -2),其中a是大于零的常数.
-2),其中a是大于零的常数.
(1)求函数f(x)的定义域.
(2)当a∈(1,4)时,求函数f(x)在[2,+∞)上的最小值.
(3)若对任意x∈[2,+∞)恒有f(x)>0,试确定a的取值范围.
|
解:(1)由x+ (*)为 (2)当1<a<4时令g(x)=x+ 因为2≤x1<x2,所以x1x2>4.即 (3)解法一: ①若0<a≤1,则当x=2时,f(2)=lg(2+ 当1<a<4,由(2)知亦使对任意x∈[2,+∞)恒有f(x)>0只要f(2)>0即lg ②当a≥4时,f(x)=lg(x+ 当x= 解法二: 因为f(x)=lg(x+ |


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知函数f(x)=2acos2x+bsinxcosx,且f(0)=2,f(![]() )=
)=![]() ,
,
(1)求使f(x)>2的x的集合;
(2)若α-β≠kπ(k∈Z),且f(α)=f(β),求tan(α+β)的值.
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知函数f(x)=x3+(m-4)x2-3mx+(n-6)(x∈R)的图象关于原点对称,m,n为实常数.
(1)求m,n的值;
(2)试用单调性的定义证明f(x)在区间[-2,2]上是单调函数
(3)当x∈[-2,2]时,不等式f(x)≥(n-logma)logma恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:龙门中学、新丰一中、连平中学三校联考试题、高三数学(理) 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:2007龙门中学、新丰一中、连平中学三校联考试题、高三数学(文) 题型:044
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com