
已知函数f(x)=(2cos2x-1)sin2x+ cos4x.
cos4x.
(1)求f(x)的最小正周期及最大值;
(2)若α∈( ,π),且f(α)=
,π),且f(α)=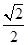 ,求α的值.
,求α的值.
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:解答题
已知函数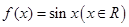 与
与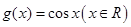 .
.
(1)对于函数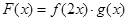 ,有下列结论:①
,有下列结论:①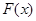 是奇函数;②
是奇函数;②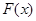 是周期函数,最小正周期为
是周期函数,最小正周期为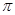 ;③
;③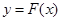 的图象关于点
的图象关于点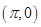 对称;④
对称;④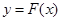 的图象关于直线
的图象关于直线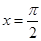 对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)
对称.其中正确结论的序号是__________;(直接写出所有正确结论的序号)
(2)对于函数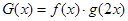 ,求满足
,求满足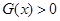 的
的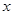 的取值范围;
的取值范围;
(3)设函数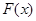 的值域为
的值域为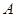 ,函数
,函数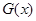 的值域为
的值域为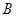 ,试判断集合
,试判断集合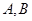 之间的关系.
之间的关系.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知a=(2cosx,cos2x),b=(sinx,- ),f(x)=a·b.
),f(x)=a·b.
(1)求f(x)的振幅、周期,并画出它在一个周期内的图象;
(2)说明它可以由函数y=sinx的图象经过怎样的变换得到.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=2sin2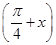 -
- cos 2x-1(x∈R).
cos 2x-1(x∈R).
(1)若函数h(x)=f(x+t)的图象关于点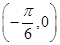 对称,且t∈(0,π),求t的值;
对称,且t∈(0,π),求t的值;
(2)设p:x∈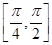 ,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.
,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=Asin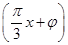 ,x∈R,A>0,0<φ<
,x∈R,A>0,0<φ<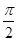 ,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).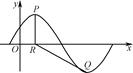
(1)求f(x)的最小正周期及φ的值;
(2)若点R的坐标为(1,0),∠PRQ=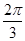 ,求A的值.
,求A的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com