
【题目】2019年![]() 月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在
月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在![]() 岁之间的
岁之间的![]() 人进行调查,经统计“年轻人”与“中老年人”的人数之比为
人进行调查,经统计“年轻人”与“中老年人”的人数之比为![]() .
.
关注 | 不关注 | 合计 | |
年轻人 |
| ||
中老年人 | |||
合计 |
|
|
|
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
(2)现已用分层抽样的办法从中老年人中选取了![]() 人进行问卷调查.若再从这
人进行问卷调查.若再从这![]() 人中选取
人中选取![]() 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的![]() 人中恰有
人中恰有![]() 人关注“中国湖北(潜江)龙虾节””的概率.
人关注“中国湖北(潜江)龙虾节””的概率.
附:参考公式![]() ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
【答案】(1)有;(2)![]() .
.
【解析】
(1)根据已知条件完成![]() 列联表,求出
列联表,求出![]() ,即可判断是否有
,即可判断是否有![]() 的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关;
的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关;
(2)现已用分层抽样的办法从中老年人中选取了![]() 人进行问卷调查,得知抽取的6位中老年人中有4人关注,2人不关注,从中选三人,写出对应的基本事件,数出满足条件的,利用概率公式求得结果.
人进行问卷调查,得知抽取的6位中老年人中有4人关注,2人不关注,从中选三人,写出对应的基本事件,数出满足条件的,利用概率公式求得结果.
(1)
关注 | 不关注 | 合计 | |
年轻人 | 10 | 30 | 40 |
中老年人 | 40 | 20 | 60 |
合计 | 50 | 50 | 100 |
其中![]() 带入公式的
带入公式的![]() ,故有
,故有![]() 的把握认为关注“中国湖北(潜江)龙虾节”和年龄段有关;
的把握认为关注“中国湖北(潜江)龙虾节”和年龄段有关;
(2)抽取的6位中老年人中有4人关注,2人不关注,设事件“选取的3人中恰有2人关注“中国湖北(潜江)龙虾节””为事件![]() ,记关注的四人为
,记关注的四人为![]() 记不关注的两人为
记不关注的两人为![]() 从这
从这![]() 人中选
人中选![]() 人的选法有
人的选法有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
共20种,其中![]() 种情况满足题意故
种情况满足题意故![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.函数 在区间
在区间![]() 上有且只有
上有且只有![]() 个零点
个零点
B.若函数![]() ,则
,则![]()
C.如果函数![]() 在
在![]() 上单调递增,那么它在
上单调递增,那么它在![]() 上单调递减
上单调递减
D.若函数![]() 的图象关于点
的图象关于点![]() 对称,则函数
对称,则函数![]() 为奇函数
为奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 上的动点,且
上的动点,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
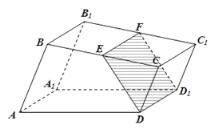
(1)证明:无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)当![]() 时,求几何体
时,求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,如图.
,如图.
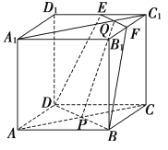
(1)若![]() 交平面
交平面![]() 于点
于点![]() ,证明:
,证明:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,若存在确定
,若存在确定![]() 的位置,若不存在说明理由.
的位置,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com