
【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为![]() .
.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
科目:高中数学 来源: 题型:
【题目】设定义在R上的函数![]() ,当
,当![]() 时,
时,![]() 取极大值
取极大值![]() ,且函数
,且函数![]() 的图象关于原点对称.
的图象关于原点对称.
(1)求![]() 的表达式;
的表达式;
(2)试在函数![]() 的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在
的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在![]() 上;
上;
(3)设![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图:

(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量
附注:
参考数据:![]() ,
,![]() ,
,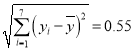 ,
,![]()
参考公式:相关系数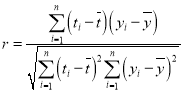 ,回归方程
,回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】前些年有些地方由于受到提高![]() 的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭,整顿,另一方面进行大量的绿化来净化和吸附污染物,通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭,整顿,另一方面进行大量的绿化来净化和吸附污染物,通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
(1)某机构随机访问50名居民,这50名居民对政府的评分(满分100分)如下表:
分数 |
|
|
|
|
|
|
频数 | 2 | 3 | 11 | 14 | 11 | 9 |
请在答题卡上作出居民对政府的评分频率分布直方图:
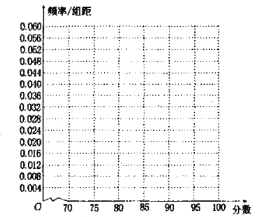
(2)当地环保部门随机抽测了2019年6月的空气质量指数,其数据如下表:
空气质量指数 | 0—50 | 50—100 | 100—150 | 150—200 |
天数 | 2 | 18 | 8 | 2 |
用空气质量指数的平均值作为该月空气质量指数级别,求出该月空气质量指数级别为第几级?(同一组数据用该组数据的区间中点值作代表,将频率视为概率)(相关知识参见附表)
(3)空气受到污染,呼吸系统等疾病患者最易感染,根据历史经验,凡遇到空气轻度污染,小李每天会服用有关药品花费50元,遇到中度污染每天服药的费用达到100元.环境整治前的2015年11月份小李因受到空气污染患呼吸系统等疾病花费了5000元,试估计2019年11月份(参考(2)中表格数据)小李比以前少花了多少钱的医药费?
附:
空气质量指数 | 0-50 | 50-100 | 100-150 | 150-200 | 200-300 | >300 |
空气质量指数级别 | I | II | III | IV | V | VI |
空气质量指数 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平而直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点、
上一点、![]() 分别是
分别是![]() 和
和![]() 上的点,求
上的点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且与直线
,且与直线![]() 相切.
相切.

(1)求椭圆的标准方程;
(2)过椭圆上点![]() 作椭圆的弦
作椭圆的弦![]() ,
,![]() ,若
,若![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,若
,若![]() 平行于
平行于![]() ,则
,则![]() ,
,![]() 斜率之和是否为定值?
斜率之和是否为定值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com