
【题目】下列函数f(x)与g(x)相等的一组是( )
A.f(x)=x﹣1,g(x)=![]() ﹣1
﹣1
B.f(x)=x2 , g(x)=(![]() )4
)4
C.f(x)=log2x2 , g(x)=2log2x
D.f(x)=tanx,g(x)=![]()
【答案】D
【解析】解:对于A,f(x)=x﹣1(x∈R),与g(x)=![]() ﹣1=x﹣1(x≠0)的定义域不同,∴不是相等函数;
﹣1=x﹣1(x≠0)的定义域不同,∴不是相等函数;
对于B,f(x)=x2(x∈R),与g(x)=(![]() )4=x2(x≥0)的定义域不同,∴不是相等函数;
)4=x2(x≥0)的定义域不同,∴不是相等函数;
对于C,f(x)=log2x2=2log2|x|(x≠0),与g(x)=2log2x(x>0)的定义域不同,对应关系也不同,∴不是相等函数;
对于D,f(x)=tanx(x≠![]() +kπ,k∈Z),与g(x)=
+kπ,k∈Z),与g(x)=![]() =tanx(x≠
=tanx(x≠![]() +kπ,k∈Z)的定义域相同,对应关系也相同,∴是相等函数.
+kπ,k∈Z)的定义域相同,对应关系也相同,∴是相等函数.
故选:D.
【考点精析】根据题目的已知条件,利用判断两个函数是否为同一函数的相关知识可以得到问题的答案,需要掌握只有定义域和对应法则二者完全相同的函数才是同一函数.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=|1﹣![]() |
|
(1)求满足f(x)=2的x值;
(2)是否存在实数a,b,且0<a<b<1,使得函数y=f(x)在区间[a,b]上的值域为[a,2b],若存在,求出a,b的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取100名市民,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
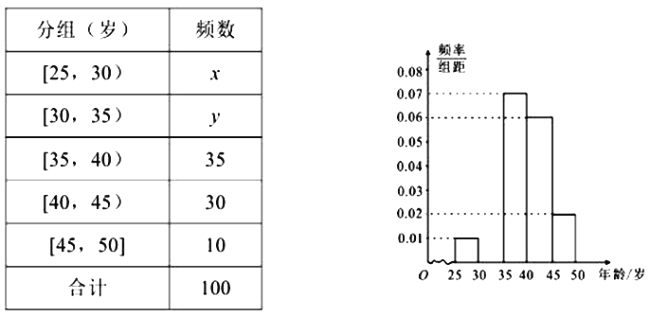
(Ⅰ)求频率分布表中![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(Ⅱ)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加国产手机用户体验问卷调查,现从这20人中随机选取2人各赠送精美礼品一份,设这2名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直线PQ与⊙O切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于Q点.
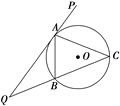
(1)求证:QC·AC=QC2-QA2;
(2)若AQ=6,AC=5,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线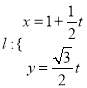 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.
求(1)三棱锥A﹣CDE的全面积;
(2)点D到平面ACE的距离.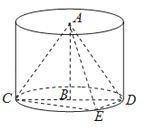
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com