
分析 根据函数的奇偶性求出a的值,求定积分的值即可.
解答 解:若f(x)=ax2+(a-2)x+a2是偶函数,
则a-2=0,即a=2,
故f(x)=2x2+4,
则${∫}_{-a}^{a}$(x2+x+$\sqrt{4-{x}^{2}}$)dx=${∫}_{-2}^{2}$x2dx+${∫}_{-2}^{2}$xdx+${∫}_{-2}^{2}$$\sqrt{4{-x}^{2}}$dx
=$\frac{1}{3}$x3${|}_{-2}^{2}$+$\frac{1}{2}$x2${|}_{-2}^{2}$+2π
=$\frac{28}{3}$+2π,
故答案为:$\frac{28}{3}$+2π.
点评 本题考查了函数的奇偶性问题,考查求定积分的值,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${x^2}-\frac{y^2}{m}=1(y≠0)$ | B. | ${x^2}-\frac{y^2}{m}=1$ | C. | ${x^2}+\frac{y^2}{m}=1(y≠0)$ | D. | ${x^2}+\frac{y^2}{m}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d<a<c<b | B. | a<c<b<d | C. | a<d<b<c | D. | a<d<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
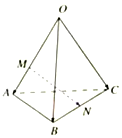 如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com