
分析 精确度是方程近似解的一个重要指标,它由计算次数决定.若初始区间是(a,b),那么经过1次取中点后,区间的长度是$\frac{b-a}{2}$,…,经过n次取中点后,区间的长度是$\frac{b-a}{{2}^{n}}$,只要这个区间的长度小于精确度m,那么这个区间内的任意一个值都可以作为方程的近似解,由此可得结论.
解答 解:初始区间是[0,4],精确度要求是0.001,需要计算的次数n满足$\frac{5-1}{{2}^{n}}$<0.001,即2n>4000,
而210=1024,211=2048,212=4096>4000,故需要计算的次数是12.
故答案为:12
点评 本题考查二分法求方程的近似解,考查学生的计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 若y=3,则y'=0 | B. | 若$y=\frac{1}{{\sqrt{x}}}$,则$y'=-\frac{{\sqrt{x}}}{2}$ | C. | 若$y=\sqrt{x}$,则$y'=\frac{1}{{2\sqrt{x}}}$ | D. | 若y=x,则y'=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
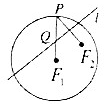 如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.
如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{16}{23}$ | B. | $-\frac{23}{16}$ | C. | $\frac{16}{23}$ | D. | $\frac{23}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $cos\frac{π}{5}$ | B. | $-cos\frac{π}{5}$ | C. | $±cos\frac{π}{5}$ | D. | $sin\frac{π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
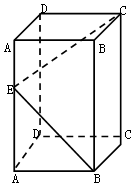 长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )
长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com