
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() :
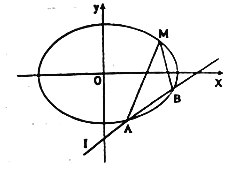
: ![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两不同的点.
两不同的点.
(1)求椭圆的方程;
(2)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() ,
, ![]() 与
与![]() 轴围成等腰三角形.
轴围成等腰三角形.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明详见解析.
;(3)证明详见解析.
【解析】试题分析:(Ⅰ)求椭圆方程采用待定系数法,首先设出椭圆方程,由离心率和点的坐标可分别得到关于![]() 的关系式,结合
的关系式,结合![]() 可求得
可求得![]() 值,从而得到椭圆方程;(Ⅱ)将直线方程与椭圆方程联立,借助于二次方程根与系数的关系可得到
值,从而得到椭圆方程;(Ⅱ)将直线方程与椭圆方程联立,借助于二次方程根与系数的关系可得到![]() 坐标与
坐标与![]() 的关系式,证明三角形为等腰三角形转化为证明直线
的关系式,证明三角形为等腰三角形转化为证明直线![]() 的斜率互为相反数,通过计算两斜率之和为0,来实现结论的证明.
的斜率互为相反数,通过计算两斜率之和为0,来实现结论的证明.
(Ⅰ)设椭圆方程为![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
又椭圆过点![]() ,所以
,所以![]() ,解得
,解得![]() ,
, ![]() ,故椭圆的方程为
,故椭圆的方程为![]()
(Ⅱ)将![]() 代入
代入![]() 并整理得
并整理得![]() ,
,
再根据![]() ,求得
,求得![]() .
.
设直线![]() ,
, ![]() 斜率分别为
斜率分别为![]() 和
和![]() ,只要证
,只要证![]() 即可.
即可.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
∴![]()
而此分式的分子等于![]()
![]()
可得![]()
因此![]() ,
, ![]() 与
与![]() 轴所围成的三角形为等腰三角形.
轴所围成的三角形为等腰三角形.


科目:高中数学 来源: 题型:
【题目】在某单位的职工食堂中,食堂每天以![]() 元/个的价格从面包店购进面包,然后以
元/个的价格从面包店购进面包,然后以![]() 元/个的价格出售.如果当天卖不完,剩下的面包以
元/个的价格出售.如果当天卖不完,剩下的面包以![]() 元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以
元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以![]() (单位:个,
(单位:个, ![]() )表示面包的需求量,
)表示面包的需求量, ![]() (单位:元)表示利润.
(单位:元)表示利润.
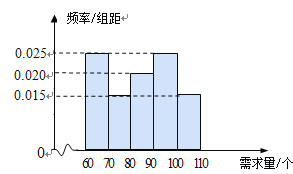
(Ⅰ)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅱ)根据直方图估计利润![]() 不少于
不少于![]() 元的概率;
元的概率;
(III)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c,当x∈R时f(x)=f(2﹣x)恒成立,且3是f(x)的一个零点. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)=f(ax)(a>1),若函数g(x)在区间[﹣1,1]上的最大值等于5,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间(0,+∞)上的函数f(x)=|t(x+ ![]() )﹣5|,其中常数t>0.
)﹣5|,其中常数t>0.
(1)若函数f(x)分别在区间(0,2),(2,+∞)上单调,试求实数t的取值范围;
(2)当t=1时,方程f(x)=m有四个不相等的实根x1 , x2 , x3 , x4 . ①求四根之积x1x2x3x4的值;
②在[1,4]上是否存在实数a,b(a<b),使得f(x)在[a,b]上单调且取值范围为[ma,mb]?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)判断性别与休闲方式是否有关系.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线的参数方程
轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线的参数方程![]() 为参数
为参数![]() )曲线
)曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数![]() 与答题正确率
与答题正确率![]() ﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
(2)若用![]() 表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间
表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间![]() 内,则强化训练有效,请问这个班的强化训练是否有效?
内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
![]() =
= ,
, ![]() =
=![]() -
-![]()
![]() ,
,
样本数据![]() 的标准差为:
的标准差为: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=mx2﹣2x+1有且仅有一个为正实数的零点,则实数m的取值范围是( )
A.(﹣∞,1]
B.(﹣∞,0]∪{1}
C.(﹣∞,0)∪(0,1]
D.(﹣∞,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com