①③
分析:根据函数y=2
x是R上的增函数可得①正确.通过举反例可得②不正确.根据奇函数的定义可得③正确.由偶函数的定义不能推出
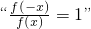
,但由
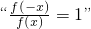
能推出
函数y=f(x)是偶函数,可得④不正确.
解答:由于函数y=2
x是R上的增函数,故由“a>b”能推出“2
a>2
b”,而且由“2
a>2
b”成立能推出“a>b”成立,故①“a>b”是“2
a>2
b”成立的充要条件,故①正确.
由②“a=b”成立不能推出“lga=lgb”成立,如a=b=-1时,“lga=lgb”不成立.但由“lga=lgb”成立,能推出“a=b”成立,故“a=b”是“lga=lgb”成立的充分不必要条件,
故②不正确.
函数f(x)=ax
2+bx(x∈R)为奇函数,等价于f(-x)=-f(x),即 ax
2 -bx=-(ax
2+bx),等价于 a=0,故函数f(x)=ax
2+bx(x∈R)为奇函数的充要条件是“a=0”,
故③正确.
由函数y=f(x)是偶函数可得 f(-x)=f(x),但不能推出
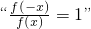
成立,(如f(x)=0时).但由
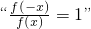
可得 f(-x)=f(x),即函数y=f(x)是偶函数,
故定义在R上的函数y=f(x)是偶函数的充分条件是
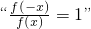
,故④不正确.
点评:本题主要考查充分条件、必要条件、充要条件的定义,函数的奇偶性可单调性,属于基础题.

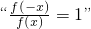 .
.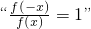 ,但由
,但由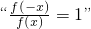 能推出
能推出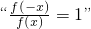 成立,(如f(x)=0时).但由
成立,(如f(x)=0时).但由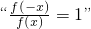 可得 f(-x)=f(x),即函数y=f(x)是偶函数,
可得 f(-x)=f(x),即函数y=f(x)是偶函数,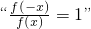 ,故④不正确.
,故④不正确.

 阅读快车系列答案
阅读快车系列答案