
 既是奇函数,又是偶函数;
既是奇函数,又是偶函数; 为同一函数;
为同一函数; 的值域为
的值域为 .
.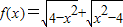 的定义域,进而得到函数的图象,结合奇偶函数图象的对称性,可判断①的真假;
的定义域,进而得到函数的图象,结合奇偶函数图象的对称性,可判断①的真假; ,结合反比例函数的单调性,可以判断③的真假;
,结合反比例函数的单调性,可以判断③的真假; =
=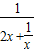 ,结合基本不等式,分类讨论函数的值域,综合讨论结果可判断④的真假.
,结合基本不等式,分类讨论函数的值域,综合讨论结果可判断④的真假.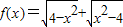 的定义域为{-2,2},其图象是点(-2,0)和(2,0),即关于原点对称也关于y轴对称,故f(x)既是奇函数,又是偶函数,即①正确;
的定义域为{-2,2},其图象是点(-2,0)和(2,0),即关于原点对称也关于y轴对称,故f(x)既是奇函数,又是偶函数,即①正确;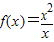 的定义域为{x|x≠0},故两者不为同一函数,故②错误;
的定义域为{x|x≠0},故两者不为同一函数,故②错误;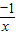 为定义在R上的奇函数,且f(x)在(0,+∞)上单调递增,但函数在(-∞,+∞)上不为增函数,故③错误;
为定义在R上的奇函数,且f(x)在(0,+∞)上单调递增,但函数在(-∞,+∞)上不为增函数,故③错误;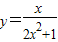 =
=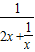
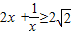 ,则y∈(0,
,则y∈(0,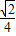 ]
]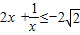 ,则y[-
,则y[-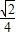 ,0)
,0)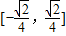 ,故④正确.
,故④正确.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆州中学高一(上)期中数学试卷(理科)(解析版) 题型:填空题
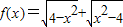 既是奇函数,又是偶函数;
既是奇函数,又是偶函数; 为同一函数;
为同一函数; 的值域为
的值域为 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆州中学高一(上)期中数学试卷(文科)(解析版) 题型:填空题
 既是奇函数,又是偶函数;
既是奇函数,又是偶函数; 为同一函数;
为同一函数; 的值域为
的值域为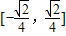 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆州中学高一(上)期中数学试卷(理科)(解析版) 题型:填空题
 既是奇函数,又是偶函数;
既是奇函数,又是偶函数; 为同一函数;
为同一函数; 的值域为
的值域为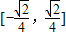 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com