
【题目】已知函数![]() ,若
,若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(I)求实数a,b的值;
(Ⅱ)证明,函数![]() 在x轴的上方无图像;
在x轴的上方无图像;
(Ⅲ)确定实数k的取值范围,使得存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
【答案】(I)![]() ,
,![]() (II)证明见解析 (Ⅲ)
(II)证明见解析 (Ⅲ)![]()
【解析】
(I)由题意得![]() ,解方程即可得解;
,解方程即可得解;
(II)构造函数![]() ,求导后证明函数
,求导后证明函数![]() 即可得证;
即可得证;
(III)由(II)知![]() 时不成立;当
时不成立;当![]() 时,由不等式的基本性质可得不符合要求;当
时,由不等式的基本性质可得不符合要求;当![]() 时,构造函数证明即可得解.
时,构造函数证明即可得解.
(I)由![]() ,则
,则![]() ,
,
又切线方程为![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 且
且![]() ,
,
![]() ,则那得:
,则那得:![]() ,
,![]() .
.
(II)由(Ⅰ)知![]() ,
,
令![]() ,
,
则![]() ,
,
令![]() 得
得![]() ,
,![]() (舍).
(舍).
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
所以当![]() 时,
时,![]() 取得最大值.
取得最大值.
即![]() .
.
所以函数![]() 在
在![]() 轴的上方无图像.
轴的上方无图像.
(III)由(II)可知,
①当![]() 时,
时,![]() ,
,
所以不存在![]() ,当
,当![]() 时,恒有
时,恒有![]() ;
;
所以![]() 不符合题意.
不符合题意.
②当![]() 时,对于
时,对于![]() ,
,![]() ,
,
所以不存在![]() ,当
,当![]() 时,恒有
时,恒有![]() 成立;
成立;
所以![]() 不符合题意.
不符合题意.
③当![]() 时,设
时,设![]() .
.
因![]() ,
,
令![]() ,即
,即![]() .
.
因为![]() ,
,
解得![]() ,
,![]()
令![]() ,则
,则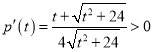 ,
,![]() 单调递增,
单调递增,
又因为![]() ,所以
,所以![]() ,
,![]() .
.
取![]() .当
.当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() .即
.即![]() .
.
所以![]() 符合题意.
符合题意.
故实数k的取值范围是![]() .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两班各派三名同学参加知识竞赛,每人回答一个问题,答对得10分,答错得0分,假设甲班三名同学答对的概率都是![]() ,乙班三名同学答对的概率分别是
,乙班三名同学答对的概率分别是![]() ,
,![]() ,
,![]() ,且这六名同学答题正确与否相互之间没有影响.
,且这六名同学答题正确与否相互之间没有影响.
(1)记“甲、乙两班总得分之和是60分”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)用![]() 表示甲班总得分,求随机变量
表示甲班总得分,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,在国家大力支持和引导下,中国遥感卫星在社会生产和生活各领域的应用范围不断扩大,中国人民用遥感卫星系统研制工作取得了显著成绩,逐步形成了气象、海洋、陆地资源和科学试验等遥感卫星系统.如图是2007—2018年中国卫星导航与位置服务产业总体产值规模(万亿)及增速(%)的统计图,则下列结论中错误的是( )
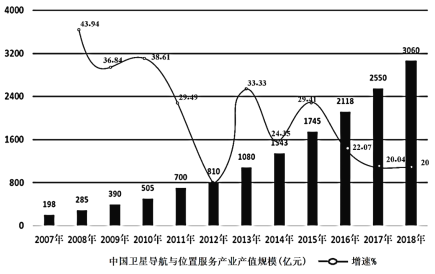
A.2017年中国卫星导航与位置服务产业总体产值规模达到2550亿元,较2016年增长20.40%
B.若2019年中国卫星导航与位置服务产业总体产值规模保持2018年的增速,总体产值规模将达3672亿元
C.2007—2018年中国卫星导航与位置服务产业总体产值规模逐年增加,但不与时间成正相关
D.2007—2018年中国卫星导航与位置服务产业总体产值规模的增速中有些与时间成负相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点坐标为
的一个焦点坐标为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,过点
,过点![]() 的直线
的直线![]() (与
(与![]() 轴不重合)与椭圆
轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,试证明:直线
,试证明:直线![]() 与
与![]() 轴平行.
轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 过点Q(1,2),F为其焦点,过F且不垂直于x轴的直线l交抛物线E于A,B两点,动点P满足△PAB的垂心为原点O.
过点Q(1,2),F为其焦点,过F且不垂直于x轴的直线l交抛物线E于A,B两点,动点P满足△PAB的垂心为原点O.
(1)求抛物线E的方程;
(2)求证:动点P在定直线m上,并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com