
如图,在△ 中,
中,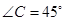 ,
, 为
为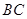 中点,
中点,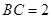 .记锐角
.记锐角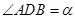 .且满足
.且满足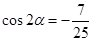 .
.
(1)求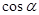 ;
;
(2)求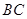 边上高的值.
边上高的值.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:解答题
如图,某城市设立以城中心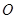 为圆心、
为圆心、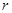 公里为半径的圆形保护区,从保护区边缘起,在城中心
公里为半径的圆形保护区,从保护区边缘起,在城中心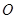 正东方向上有一条高速公路
正东方向上有一条高速公路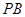 、西南方向上有一条一级公路
、西南方向上有一条一级公路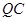 ,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆
,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆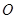 相切的直道
相切的直道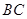 .已知通往一级公路的道路
.已知通往一级公路的道路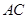 每公里造价为
每公里造价为 万元,通往高速公路的道路
万元,通往高速公路的道路 每公里造价是
每公里造价是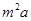 万元,其中
万元,其中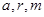 为常数,设
为常数,设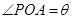 ,总造价为
,总造价为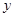 万元.
万元.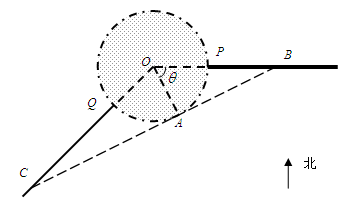
(1)把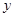 表示成
表示成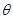 的函数
的函数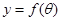 ,并求出定义域;
,并求出定义域;
(2)当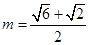 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com