
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的图象的相邻两对称中心的距离为π,且f(x+
)的图象的相邻两对称中心的距离为π,且f(x+ ![]() )=f(﹣x),则函数y=f(
)=f(﹣x),则函数y=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函数且在x=0处取得最大值
B.偶函数且在x=0处取得最小值
C.奇函数且在x=0处取得最大值
D.奇函数且在x=0处取得最小值
【答案】A
【解析】解:∵函数f(x)=Asin(ωx+φ)的图象的相邻两对称中心的距离为π, 即 ![]() ,
,
∴T=2π,于是 ![]() .
.
∴f(x)=Asin(x+φ);
由f(x+ ![]() )=f(﹣x),得:Asin(x+
)=f(﹣x),得:Asin(x+ ![]() +φ)=Asin(﹣x+φ),
+φ)=Asin(﹣x+φ),
∴x+ ![]() +φ﹣x+φ=π+2kπ,即φ=
+φ﹣x+φ=π+2kπ,即φ= ![]() .
.
取k=0,得φ= ![]() ,
,
∴f(x)=Asin(x+ ![]() ),
),
则y=f( ![]() ﹣x)=Asin(
﹣x)=Asin( ![]() x+
x+ ![]() )=Acosx,A>0,
)=Acosx,A>0,
∴函数y=f( ![]() ﹣x)是偶函数且在x=0处取得最大值.
﹣x)是偶函数且在x=0处取得最大值.
故选:A.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥AD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点,DE=EC. 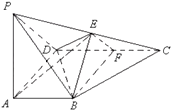
(1)求证:平面ABE⊥平面BEF;
(2)设PA=a,若平面EBD与平面ABCD所成锐二面角 ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() ,﹣1),
,﹣1), ![]() =(
=( ![]() sin
sin ![]() ,cos2
,cos2 ![]() ),设函数f(x)=
),设函数f(x)= ![]() +1.
+1.
(1)若x∈[0, ![]() ],f(x)=
],f(x)= ![]() ,求cosx的值;
,求cosx的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足2bcosA≤2c﹣ ![]() a,求f(B)的取值范围.
a,求f(B)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.

(1)若QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(2)如果∠AOQ=60°,QB=2![]() ,求此圆锥的体积.
,求此圆锥的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1n(x﹣1)﹣k(x﹣1)+1
(1)求函数f(x)的单调区间;
(2)若f(x)≤0恒成立,试确定实数k的取值范围;
(3)证明: ![]() 且n>1)
且n>1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2016x+log2016( ![]() +x)﹣2016﹣x+2,则关于x的不等式f(3x+1)+f(x)>4的解集为( )
+x)﹣2016﹣x+2,则关于x的不等式f(3x+1)+f(x)>4的解集为( )
A.(﹣ ![]() ,+∞)
,+∞)
B.(﹣∞,﹣ ![]() )
)
C.(0,+∞)
D.(﹣∞,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,若将f(x)图象上的所有点向右平移
)的部分图象如图所示,若将f(x)图象上的所有点向右平移 ![]() 个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( )
个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( ) 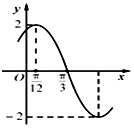
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
B.[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z
],k∈Z
C.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
D.[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z
],k∈Z
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com