
分析 当P点在直线l与过点A,B的直线的交叉点处时,它到A、B两点的距离之差最大为AB,求出过点A(3,4),B(11,0)的直线方程,与直线l:y=2x+3联立方程组,能求出P点坐标及最大值.
解答 解:∵三角形两边之和必大于第三边,反之两边之差必小于第三边,
若PAB为三角形,则pA与pB之差必小于AB;
若P、A、B在一条直线上(P点不在线段AB内),则PA与PB之差为AB,
故当P点在直线l与过点A,B的直线的交叉点处时,
它到A、B两点的距离之差最大为AB,
过点A(3,4),B(11,0)的直线方程为:$\frac{y}{x-11}=\frac{4}{3-11}$,
整理,得:x+2y-11=0,
与直线L:y=2x+3联立方程组$\left\{\begin{array}{l}{x+2y-11=0}\\{y=2x+3}\end{array}\right.$,解得x=1,y=5,
故P点坐标为P(1,5),
∴使点P到A、B距离之差最大,P点坐标为(1,5),
点P到A、B距离之差最大值:|AB|=$\sqrt{(3-11)^{2}+(4-0)^{2}}$=4$\sqrt{5}$.
点评 本题考查使点P到A、B距离之差最大的P点坐标及最大值的求法,解题时要认真审题,注意直线方程与两点间距离公式的合理运用,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,$x+\frac{1}{x}>a$成立 | B. | ?x∈R,$x+\frac{1}{x}<a$成立 | C. | ?x∈R,$x+\frac{1}{x}≥a$成立 | D. | ?x∈R,$x+\frac{1}{x}≤a$成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
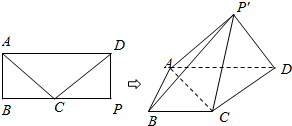 已知矩形ABPD,点C为BP的中点,AD=2,AB=1,将△CDP沿CD折起成四棱锥P′-ABCD,其中∠AP′D=90°
已知矩形ABPD,点C为BP的中点,AD=2,AB=1,将△CDP沿CD折起成四棱锥P′-ABCD,其中∠AP′D=90°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com