
【题目】△ABC的三边长是三个连续的自然数,且最大角是最小角的2倍,则此三角形的面积为______.
【答案】![]()
【解析】
根据三角形满足的两个条件,设出三边长分别为n-1,n,n+1,三个角分别为α,π-3α,2α,由n-1,n+1,sinα,以及sin2α,利用正弦定理列出关系式,根据二倍角的正弦函数公式化简后,表示出cosα,然后利用余弦定理得到(n-1)2=(n+1)2+n2-2(n-1)ncosα,将表示出的cosα代入,整理后得到关于n的方程,求出方程的解得到n的值,从而得到三边长的值,最后求三角形的面积.
解:设三角形三边是连续的三个自然n-1,n,n+1,三个角分别为α,π-3α,2α,
由正弦定理可得:![]() ,
,
∴cosα=![]() ,
,
再由余弦定理可得:(n-1)2=(n+1)2+n2-2(n+1)ncosα=(n+1)2+n2-2(n+1)n![]() ,
,
化简可得:n2-5n=0,解得:n=5或n=0(舍去),
∴n=5,故三角形的三边长分别为:4,5,6.
所以cosα=![]() ,
,
所以S=![]() .
.
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】下列是关于复数的类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由实数绝对值的性质|x|2=x2类比得到复数z的性质|z|2=z2;
③已知a,b∈R,若a-b>0,则a>b类比得已知z1,z2∈C,若z1-z2>0,则z1>z2;
④由向量加法的几何意义可以类比得到复数加法的几何意义.
其中推理结论正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(I)求函数在点(1,0)处的切线方程;
(II)设实数k使得f(x)< kx恒成立,求k的范围;
(III)设函数![]() ,求函数h(x)在区间
,求函数h(x)在区间![]() 上的零点个数.
上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
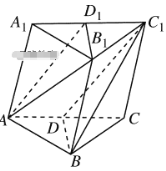
【题目】如图所示,在斜三棱柱ABC—A1B1C1中,点D,D1分别为AC,A1C1上的点.
(1)当![]() 的值等于何值时,BC1∥平面AB1D1;
的值等于何值时,BC1∥平面AB1D1;
(2)若平面BC1D∥平面AB1D1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD的边AB=2,BC=1,以A为坐标原点,AB,AD边分别在x轴、y轴的正半轴上,建立直角坐标系。将矩形折叠,使A点落在线段DC上,重新记为点![]()
(1)当点![]() 坐标为(1,1)时,求折痕所在直线方程.
坐标为(1,1)时,求折痕所在直线方程.
(2)若折痕所在直线的斜率为k,试求折痕所在直线的方程;
(3)当![]() 时,设折痕所在直线与
时,设折痕所在直线与![]() 轴交于点E,与
轴交于点E,与![]() 轴交于点F,将
轴交于点F,将![]() 沿折痕EF旋转.使二面角
沿折痕EF旋转.使二面角![]() 的大小为
的大小为![]() ,设三棱锥
,设三棱锥![]() 的外接球表面积为
的外接球表面积为![]() ,试求
,试求![]() 最小值.
最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com