
分析 可将原函数变成$y=-({2}^{x})^{2}+\frac{1}{2}•{2}^{x}+1$,可以看出定义域为R,然后可配方,根据2x>0便可得出原函数的值域.
解答 解:$y=-{4}^{x}+(\frac{1}{2})^{1-x}+1=-({2}^{x})^{2}+\frac{1}{2}•{2}^{x}+1$=$-({2}^{x}-\frac{1}{4})^{2}+\frac{17}{16}$;
∴该函数的定义域为R;
∵2x>0;
∴$-({2}^{x}-\frac{1}{4})^{2}+\frac{17}{16}≥\frac{17}{16}$;
∴该函数的值域为[$\frac{17}{16}$,+∞).
点评 考查函数定义域、值域的概念,配方求二次式子取值范围的方法,以及指数函数的值域.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
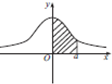 如图是正态分布N(0,1)的正态曲线图,下面4个式子中(注:Φ(a)=P(X≤a)),等于图中阴影部分的面积的个数为( )
如图是正态分布N(0,1)的正态曲线图,下面4个式子中(注:Φ(a)=P(X≤a)),等于图中阴影部分的面积的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com