
分析 (I)n=5时,A═{3,32,33,34,35},从中选出3个不同的数,使这3个数按一定的顺序排列构成等比数列,则共有3,32,33;32,33,34;33,34,35;3,33,35.其顺序反过来也成立.可得f(5).
(II)A={3,32,33,…,3n}(n≥3),公比为3的共有:n-2个;公比为的共有:n-2个.公比为32的共有:n-4个;公比为的共有:n-4个.…,则f(n)=220=2[(n-2)+(n-4)+…2],即可得出.
解答 解:(I)n=5时,A═{3,32,33,34,35},从中选出3个不同的数,使这3个数按一定的顺序排列构成等比数列,则共有3,32,33;32,33,34;33,34,35;3,33,35.其顺序反过来也成立.因此f(5)=8.
(II)A={3,32,33,…,3n}(n≥3),
公比为3的共有:n-2个;公比为的共有:n-2个.
公比为32的共有:n-4个;公比为的共有:n-4个.
…,
则f(n)=220=2[(n-2)+(n-4)+…2],
∴,n2-2n-440=0,
解得n=22.
故答案为:8,22.
点评 本题考查了等差数列与等比数列的通项公式求和公式及其性质,考查了分类讨论方法、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
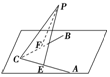 ∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2 cm,那么PC与平面ABC所成角的大小为45°.
∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2 cm,那么PC与平面ABC所成角的大小为45°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com