
分析 (1)a=1时,得出命题p:x>2,或x<0,命题q:-2<x<3,而由p∧q为真得到p,q都为真,从而解不等式组$\left\{\begin{array}{l}{x>2,或x<0}\\{-2<x<3}\end{array}\right.$即得实数x的取值范围;
(2)先求出命题¬p:x<1-a,或x>1+a,a>0,从而由¬p是q的必要不充分条件得到$\left\{\begin{array}{l}{a>0}\\{a+1≥3}\\{1-a≤-2}\end{array}\right.$,解该不等式组即得实数a的取值范围.
解答 解:(1)当a=1时,p:x>2或x<0,q:-2<x<3;
又p∧q真,∴p,q都为真;
∴由$\left\{{\begin{array}{l}{x>2或x<0}\\{-2<x<3}\end{array}}\right.$得-2<x<0或2<x<3;
∴实数x取值范围为(-2,0)∪(2,3);
(2)p:|x-1|>a,∴x<1-a或x>1+a,a>0,¬p:1-a≤x≤1+a,a>0;
∵¬p是q的必要不充分条件;
∴$\left\{\begin{array}{l}{a>0}\\{a+1≥3}\\{1-a≤-2}\end{array}\right.$;
∴a≥3;
∴实数a的取值范围为[3,+∞).
点评 考查含绝对值不等式的解法,根据指数函数的单调性解不等式,一元二次不等式的解法,以及由命题p能写出命题¬p,必要不充分条件的概念.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
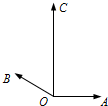 如图,平面内有三个向量$\overrightarrow{OA},\;\overrightarrow{OB},\;\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为150°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为90°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}\;(λ,μ∈R)$,则λ+μ=( )
如图,平面内有三个向量$\overrightarrow{OA},\;\overrightarrow{OB},\;\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为150°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为90°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}\;(λ,μ∈R)$,则λ+μ=( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$+2 | D. | 2$\sqrt{3}$+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
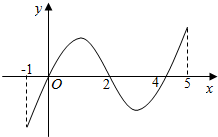 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.下列四个命题:| x | -1 | 0 | 4 | 5 |
| f(x) | -1 | -2 | -2 | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
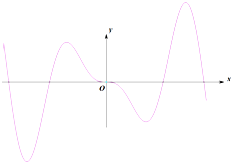
| A. | f(x)=xcosx-sinx | B. | f(x)=xsinx | C. | f(x)=xcosx+sinx | D. | f(x)=xcosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),
将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 归纳推理 | B. | 类比推理 | C. | 演绎推理 | D. | 以上均有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com