分析:(1)以O为坐标原点OB、OC、OF为x、y、z轴建立空间直角坐标系,由已知中ABC-A
1B
1C
1是正三棱柱,AB=2,AA
1=3,C
1E=2,我们分别求出向量
,
,
的坐标,根据
•=0•=0,得到DC⊥AB、DC⊥AE,进而由线面垂直的判定定理得到答案.
(2)分别求出平面ABE与平面ADE的法向量,代入向量夹角公式,即可得到二面角D-AE-B的余弦值,进而得到二面角D-AE-B的大小.
解答: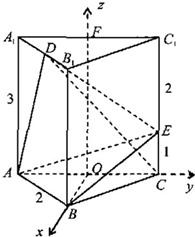
解:(1)证明:已知ABC-A
1B
1C
1是正三棱柱,取AC中点O、A
1C
1中点F,连OF、OB,则OB、OC、OF两两垂直,
以OB、OC、OF为x、y、z轴建立空间直角坐标系.如图所示.
∵AB=2,AA
1=3,C
1E=2
∴A(0,-1,0),
B(,0,0),E(0,1,1),C(0,1,0),
D(,-,3)∴
=(-,,-3),
=(,1,0),
=(0,2,1)∴
•=0,
•=0于是,有DC⊥AB、DC⊥AE.
又因AB与AE相交,故DC⊥面ABE.(6分)
(2)由(1)得
=(-,,-3)为平面ABE的一个法向量
设
=(x,y,z)为平面ADE的一个法向量
则
,
即
令y=1,则
=(
,1,-2)
令二面角D-AE-B的平面角为θ
则cosθ=
∴二面角D-AE-B的大小
θ=arccos(12分)
点评:本题考查的知识点是二面角的平面角及求法,直线与平面垂直的判定,其中建立空间坐标系,将直线与平面的垂直问题,二面角问题,转化为空间向量夹角问题是解答本题的关键.


 解:(1)证明:已知ABC-A1B1C1是正三棱柱,取AC中点O、A1C1中点F,连OF、OB,则OB、OC、OF两两垂直,
解:(1)证明:已知ABC-A1B1C1是正三棱柱,取AC中点O、A1C1中点F,连OF、OB,则OB、OC、OF两两垂直,

 名校课堂系列答案
名校课堂系列答案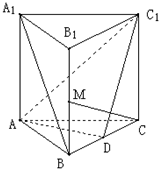 如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M 是棱BB1的中点,又CM⊥AC1,
如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M 是棱BB1的中点,又CM⊥AC1,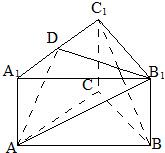 如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为
如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为 如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M在棱BB1上,且BM=
如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M在棱BB1上,且BM= (2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.
(2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.