��2012•��ͷһģ������A��B������Ŀ��Ͷ��A��Ŀ100��Ԫ��һ����õ�����Ϊ�������X
1����Ԫ���������г�������X
1�ķֲ���Ϊ��
Ͷ��B��Ŀ100��Ԫ��һ����õ�����X
2����Ԫ����B��Ŀ��Ʒ�۸�ĵ������۸��ϵ����µ����йأ���֪B��Ŀ��Ʒ�۸���һ���ڽ���2�ζ����ĵ���������ÿ�ε����м۸��µ��ĸ��ʶ���p��0��p��1����
��ר�Ҳ�������B��Ŀ��Ʒ�۸���µ���һ�������Ӧ����Ĺ�ϵ���±���
| B��Ŀ��Ʒ�۸�һ�����µ�����X���Σ� |
0 |
1 |
2 |
| Ͷ��100��Ԫһ����õ�����X2����Ԫ�� |
13 |
12.5 |
2 |
������X
1�ķ���D��X
1����
������X
2�ķֲ��У�
������p=0.3������Ͷ�ʻ������IJ��죬��Ը��ѡ��Ͷ���ĸ���Ŀ��
���ο����ݣ�1.2
2��0.49+0.7
2��0.42+9.8
2��0.09=9.555����



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
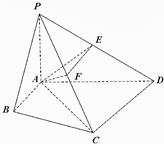 ��2012•��ͷһģ��������P-ABCD�У���ABC=��ACD=90�㣬��BAC=��CAD=60�㣬PA��ƽ��ABCD��EΪPD���е㣬PA=2��AB=1��
��2012•��ͷһģ��������P-ABCD�У���ABC=��ACD=90�㣬��BAC=��CAD=60�㣬PA��ƽ��ABCD��EΪPD���е㣬PA=2��AB=1�� ��2012•��ͷһģ������f��x��=sin����x+?��������|?|��
��2012•��ͷһģ������f��x��=sin����x+?��������|?|��