设由正数组成的等比数列,公比q=2,且a1•a2…a30=230,则a3•a6•a9…a30等于
【答案】
分析:先用a
3表示出a
1,a
2,用a
6表示出a
4,a
5,…,用a
30表示出a
28,a
29,然后代入a
1•a
2…a
30=2
30,可得到a
3•a
6•a
9…a
30的值.
解答:解:∵a
1=
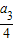
,a
2=
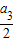
,a
4=
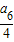
,a
5=
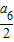
,…,a
28=
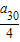
,a
29=
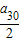
由a
1a
2…a
30=2
30得
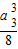
×

×…×
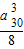
=2
30于是(a
3•a
6…a
30)
3=2
30×8
10=2
60
所以
a
3a
6…a
30=2
20
故答案为2
20.
点评:本题主要考查等比数列的基本性质.属基础题.
