
分析 由已知及三角函数恒等变换的应用化简可得y=-$\frac{1}{2}$sin(α-β)-$\frac{1}{2}$,由已知可得-$\frac{π}{4}$≤α-β≤π,利用正弦函数的图象和性质可得-$\frac{\sqrt{2}}{2}$≤sin(α-β)≤1,即可得解.
解答 解:∵α+β=$\frac{2π}{3}$,
∴y=$\frac{1-cos(π-2α)}{cot\frac{α}{2}-tan\frac{α}{2}}$-cos2($\frac{π}{4}$-β)=$\frac{1+cos2α}{\frac{co{s}^{2}\frac{α}{2}-si{n}^{2}\frac{α}{2}}{sin\frac{α}{2}cos\frac{α}{2}}}$-$\frac{1+cos(\frac{π}{2}-2β)}{2}$=$\frac{1+cos2α}{\frac{cosα}{\frac{1}{2}sinα}}$-$\frac{1}{2}$-sin2β=$\frac{(1+cos2α)sinα}{2cosα}$-$\frac{1}{2}$-$\frac{1}{2}$sin2β
=$\frac{1}{2}$sin2α-$\frac{1}{2}$-$\frac{1}{2}$sin2β=$\frac{1}{2}$(sin2α-sin2β)-$\frac{1}{2}$=cos(α+β)sin(α-β)-$\frac{1}{2}$
=-$\frac{1}{2}$sin(α-β)-$\frac{1}{2}$,
∵0≤α≤π,0≤β≤$\frac{π}{4}$,∴-$\frac{π}{4}$≤α-β≤π,
∴-$\frac{\sqrt{2}}{2}$≤sin(α-β)≤1,
∴y=-$\frac{1}{2}$sin(α-β)-$\frac{1}{2}$∈[-1,$\frac{\sqrt{2}-2}{4}$],
∴当α=0,β=$\frac{π}{4}$时,y=$\frac{1-cos(π-2α)}{cot\frac{α}{2}-tan\frac{α}{2}}$-cos2($\frac{π}{4}$-β)的最大值为:$\frac{\sqrt{2}-2}{4}$.
点评 本题主要考查了正弦函数的图象和性质,三角函数恒等变换的应用,考查了计算能力和转化思想,属于中档题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:选择题
| A. | k>1 | B. | $k>\frac{1}{3}$ | C. | $k>\frac{1}{5}$ | D. | $k>\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
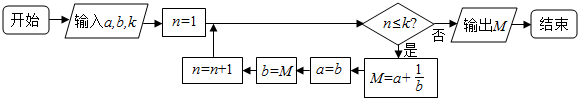
| A. | $\frac{4}{3}$ | B. | $\frac{8}{5}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
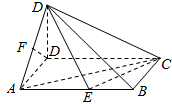 如图,四边形ABCD为矩形,DD1⊥底面ABCD,AD=DD1=$\frac{1}{2}$AB,点F为AD1的中点.点E在棱AB上移动.
如图,四边形ABCD为矩形,DD1⊥底面ABCD,AD=DD1=$\frac{1}{2}$AB,点F为AD1的中点.点E在棱AB上移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com