解:(1)由题意,对任意x∈R,f(-x)=-f(x),
即a
-x-(k-1)a
x=-a
x+(k-1)a
-x,
即(k-1)(a
x+a
-x)-(a
x+a
-x)=0,(k-2)(a
x+a
-x)=0,
因为x为任意实数,所以k=2.
解法二:因为f(x)是定义域为R的奇函数,所以f(0)=0,即1-(k-1)=0,k=2.
当k=2时,f(x)=a
x-a
-x,f(-x)=a
-x-a
x=-f(x),f(x)是奇函数.
所以k的值为2.
(2)(理)由(1)f(x)=a
x-a
-x,因为
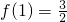
,所以
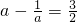
,
解得a=2.
故f(x)=2
x-2
-x,g(x)=2
2x+2
-2x-2m(2
x-2
-x),
令t=2
x-2
-x,则2
2x+2
-2x=t
2+2,由x∈[1,+∞),得
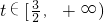
,
所以g(x)=h(t)=t
2-2mt+2=(t-m)
2+2-m
2,
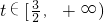
当

时,h(t)在
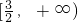
上是增函数,则
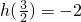
,

,
解得

(舍去).
当
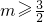
时,则f(m)=-2,2-m
2=-2,解得m=2,或m=-2(舍去).
综上,m的值是2.
(2)(文)由(1)知f(x)=a
x-a
-x,由f(1)<0,得
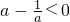
,解得0<a<1.
当0<a<1时,y=a
x是减函数,y=-a
-x也是减函数,所以f(x)=a
x-a
-x是减函数.
由f(x
2+tx)+f(4-x)<0,所以f(x
2+tx)<-f(4-x),
因为f(x)是奇函数,所以f(x
2+tx)<f(x-4).
因为f(x)是R上的减函数,所以x
2+tx>x-4即x
2+(t-1)x+4>0对任意x∈R成立,
所以△=(t-1)
2-16<0,
解得-3<t<5.
所以,t的取值范围是(-3,5).
分析:(1)根据奇函数的定义:对任意x∈R,f(-x)=-f(x),或性质可得f(0)=0,由此求得k值.
(2)(理)利用换元法,将函数转化为二次函数,研究函数的单调性,得到函数g(x)取得最小值.利用条件,就可以求m的值.
(文)由f(x)=a
x-a
-x(a>0且a≠1),f(1)<0,求得0<a<1,f(x)在R上单调递减,不等式化为f(x
2+tx)<f(x-4),即x
2+(t-1)x+4>0 恒成立,由△<0求得t的取值范围.
点评:本题考查指数型复合函数的性质以及应用,考查函数的奇偶性的应用,属于中档题.

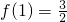 ,且g(x)=a2x+a-2x-2m•f(x)在[1,+∞)上的最小值为-2,求m的值.
,且g(x)=a2x+a-2x-2m•f(x)在[1,+∞)上的最小值为-2,求m的值.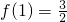 ,所以
,所以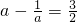 ,
,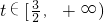 ,
,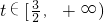
 时,h(t)在
时,h(t)在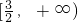 上是增函数,则
上是增函数,则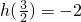 ,
, ,
, (舍去).
(舍去).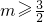 时,则f(m)=-2,2-m2=-2,解得m=2,或m=-2(舍去).
时,则f(m)=-2,2-m2=-2,解得m=2,或m=-2(舍去).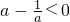 ,解得0<a<1.
,解得0<a<1.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案 设函数f(x)=(a
设函数f(x)=(a