
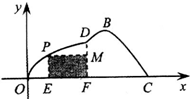
 如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< ),x∈[4,8]时的图象,图象的最高点为B(5,
),x∈[4,8]时的图象,图象的最高点为B(5, ),DF⊥OC,垂足为F.
),DF⊥OC,垂足为F. ,ω=
,ω= =
=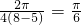 ,
, ),代入y=
),代入y= sin(
sin( x+φ)得:
x+φ)得: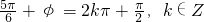 ,
, ,所以φ=
,所以φ= ,所以函数的解析式为y=
,所以函数的解析式为y= sin(
sin( x
x ).
). sin(
sin( x
x )中,令x=4,得D(4,4)
)中,令x=4,得D(4,4)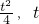 )(0≤t≤4),则矩形PMFE的面积为S=
)(0≤t≤4),则矩形PMFE的面积为S=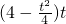 ,0≤t≤4.
,0≤t≤4.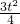 ,由S′=0得t=
,由S′=0得t= ,且t∈
,且t∈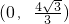 时S′>0,S递增,
时S′>0,S递增,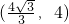 时S′<0,S递减,
时S′<0,S递减, ,S最大,此时点P的坐标
,S最大,此时点P的坐标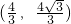 .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
 (2011•盐城二模)如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
(2011•盐城二模)如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| 8 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市安溪八中高三(上)12月月考数学试卷(理科)(解析版) 题型:解答题
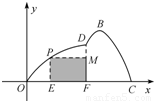 如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<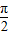 ),x∈[4,8]时的图象,图象的最高点为B(5,
),x∈[4,8]时的图象,图象的最高点为B(5,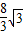 ),DF⊥OC,垂足为F.
),DF⊥OC,垂足为F.查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省泰安市高三(上)期末数学试卷(文科)(解析版) 题型:解答题
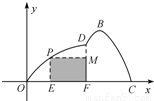 如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<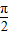 ),x∈[4,8]时的图象,图象的最高点为B(5,
),x∈[4,8]时的图象,图象的最高点为B(5,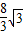 ),DF⊥OC,垂足为F.
),DF⊥OC,垂足为F.查看答案和解析>>
科目:高中数学 来源:2011年江苏省盐城市高考数学二模试卷(解析版) 题型:解答题
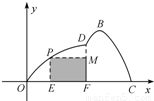 如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<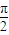 ),x∈[4,8]时的图象,图象的最高点为B(5,
),x∈[4,8]时的图象,图象的最高点为B(5,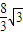 ),DF⊥OC,垂足为F.
),DF⊥OC,垂足为F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com