
 如图所示,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,设M是上底面A1B1C1D1的中心.
如图所示,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,设M是上底面A1B1C1D1的中心.分析 根据平行六面体中的相等向量或相反向量,利用向量的运算法则,进行化简即可.
解答 解:(1)在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,M是上底面A1B1C1D1的中心;
∴$\overrightarrow{A{A}_{1}}$+$\frac{1}{2}$($\overrightarrow{AD}$+$\overrightarrow{AB}$)=$\overrightarrow{A{A}_{1}}$+$\frac{1}{2}$($\overrightarrow{{{A}_{1}B}_{1}}$+$\overrightarrow{{{A}_{1}D}_{1}}$)
=$\overrightarrow{{AA}_{1}}$+$\frac{1}{2}$$\overrightarrow{{{A}_{1}C}_{1}}$
=$\overrightarrow{A{A}_{1}}$+$\overrightarrow{{A}_{1}M}$
=$\overrightarrow{AM}$;
(2)∵$\overrightarrow{BM}$=$\overrightarrow{{BB}_{1}}$+$\overrightarrow{{B}_{1}M}$
=$\overrightarrow{{AA}_{1}}$+$\frac{1}{2}$$\overrightarrow{{{B}_{1}D}_{1}}$
=$\overrightarrow{{AA}_{1}}$+$\frac{1}{2}$($\overrightarrow{{{B}_{1}A}_{1}}$+$\overrightarrow{{{B}_{1}C}_{1}}$)
=$\overrightarrow{{AA}_{1}}$+$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{BC}$)
=$\overrightarrow{{AA}_{1}}$+$\frac{1}{2}$(-$\overrightarrow{AB}$+$\overrightarrow{AD}$)
=-$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$+$\overrightarrow{{AA}_{1}}$,
且$\overrightarrow{BM}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,
∴x=-$\frac{1}{2}$,y=$\frac{1}{2}$,z=1.
点评 本题考查了相等向量与相反向量以及向量线性运算法则的应用问题,是基础题目.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
| n | n≥59% | 50%≤n<59% | 40%≤n<50% | 30%≤n<40% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
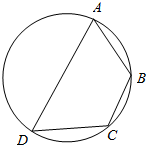 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论:
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com