
 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:| A. | ①④ | B. | ②④ | C. | ②③ | D. | ③④ |
分析 根据导函数图象可判定导函数的符号,从而确定函数的单调性,得到极值点,以及根据导数的几何意义可知在某点处的导数即为在该点处的切线斜率.
解答 解:根据导函数图象可知当x∈(-∞,-3)时,f'(x)<0,在x∈(-3,1)时,f'(x)≥0,
∴函数y=f(x)在(-∞,-3)上单调递减,在(-3,1)上单调递增,故④正确;
-3是函数y=f(x)的极小值点,当f(-3)<0时,函数y=f(x)有两个相异的零点,故①错误;
∵在(-3,1)上单调递增∴-1不是函数y=f(x)的最小值点,
∴函数y=f(x)只有一个极值点,故②正确;
∵函数y=f(x)在x=0处的导数大于0,∴切线的斜率大于零,故③不正确;
故②④正确,
故选:B.
点评 本题主要考查了导函数图象与函数的性质的关系,以及函数的单调性、极值、和切线的斜率等有关知识,属于中档题.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|$\frac{1}{a}$<x<1} | B. | {x|-1<x<$\frac{1}{a}$} | C. | {x|1$<x<\frac{1}{a}$} | D. | {x|-$\frac{1}{a}$<x<-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
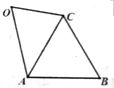 已知a,b,c分别是△ABC的内角A,B,C所对的边长,a=c,且满足bsinA=$\sqrt{3}$acosB.点O为△ABC外一点,OA=2OC=4,求平面四边形ABCO的面积的最大值.
已知a,b,c分别是△ABC的内角A,B,C所对的边长,a=c,且满足bsinA=$\sqrt{3}$acosB.点O为△ABC外一点,OA=2OC=4,求平面四边形ABCO的面积的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
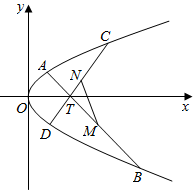 已知抛物线E:y2=2px(p>0)的焦点为F,抛物线上存在一点P到其焦点的距离为$\frac{3}{2}$,且点P在圆x2+y2=$\frac{9}{4}$上.
已知抛物线E:y2=2px(p>0)的焦点为F,抛物线上存在一点P到其焦点的距离为$\frac{3}{2}$,且点P在圆x2+y2=$\frac{9}{4}$上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com