
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0 时,有 ![]() .
.
(1)求证:f(x)在[﹣1,1]上为增函数;
(2)求不等式 ![]() 的解集;
的解集;
(3)若 ![]() 对所有
对所有 ![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
【答案】
(1)解:证明:任取x1,x2∈[﹣1,1]且x1<x2,则 ![]() ,
,
∴f(x2)>f(x1),∴f(x)为增函数
(2)解: ![]() ,等价于
,等价于 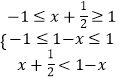 ,求得0≤x<
,求得0≤x< ![]() ,
,
即不等式 ![]() 的解集为
的解集为 ![]()
(3)解:由于f(x)为增函数,
∴f(x)的最大值为 ![]() 对
对 ![]() 恒成立
恒成立 ![]() 对
对 ![]() 的恒成立,
的恒成立,
设 ![]() ,则
,则 ![]() .
.
又 ![]() =
= ![]() =1+tan2α+2tanα+2=(tanα+1)2+2,
=1+tan2α+2tanα+2=(tanα+1)2+2,
∵α∈[﹣ ![]() ,
, ![]() ],∴tanα∈[﹣
],∴tanα∈[﹣ ![]() ,1],故当tanα=1时,
,1],故当tanα=1时,
![]()
∴t2+t≥6,求得t≤﹣3 t≥2,即为所求的实数t的取值范围.
【解析】(1)由条件利用增函数的定义证得结论.(2)根据函数的奇偶性和单调性,把要解的不等式等价转化为一个不等式组,求得此不等式的解集即可.(3)根据函数的单调性求得f(x)的最大值,可得t2+t≥g(α)= ![]() +2tanα+2 对
+2tanα+2 对 ![]() 的恒成立,再求得g(α)的最大值,从而求得t的范围.
的恒成立,再求得g(α)的最大值,从而求得t的范围.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值),还要掌握函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇)的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=ax﹣lnx,x∈(0,e],其中e是自然常数,a∈R.
(1)当a=1时,求f(x)的单调区间和极值;
(2)是否存在实数a,使f(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
(3)证明:(1﹣ ![]() )(
)( ![]() )(
)( ![]() ﹣
﹣ ![]() )…(
)…( ![]() ﹣
﹣ ![]() )<e3(3﹣n) .
)<e3(3﹣n) .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘成折线图如下:
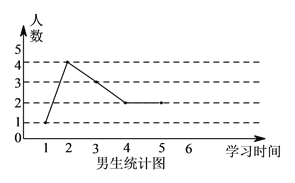
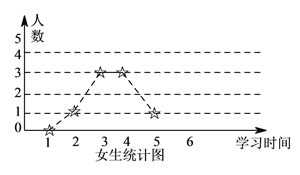
(I)已知该校有![]() 名学生,试估计全校学生中,每天学习不足
名学生,试估计全校学生中,每天学习不足![]() 小时的人数.
小时的人数.
(II)若从学习时间不少于![]() 小时的学生中选取
小时的学生中选取![]() 人,设选到的男生人数为
人,设选到的男生人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
(III)试比较男生学习时间的方差![]() 与女生学习时间方差
与女生学习时间方差![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
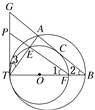
【题目】如图所示,两圆内切于点T,大圆的弦AB切小圆于点C.TA,TB与小圆分别相交于点E,F.FE的延长线交两圆的公切线TP于点P.
求证:(1) ![]() =
=![]() ;
;
(2)AC·PF=BC·PT.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)求函数f(x)的最小正周期和图象的对称轴方程.
(2)求函数f(x)的单调增区间.
(3)求函数y=f(x)在区间 ![]() 上的最小值,并求使y=f(x)取得最小值时的x的值.
上的最小值,并求使y=f(x)取得最小值时的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() 是椭圆
是椭圆![]() 上的两点,椭圆的离心率为
上的两点,椭圆的离心率为![]() ,短轴长为2,已知向量
,短轴长为2,已知向量![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆的焦点
过椭圆的焦点![]() ,(
,( ![]() 为半焦距),求直线
为半焦距),求直线![]() 的斜率
的斜率![]() 的值;
的值;
(2)试问: ![]() 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(0,+∞),f(2)=1,f(xy)=f(x)+f(y)且当x>1时,f(x)>0.
(1)判断函数f(x)在其定义域(0,+∞)上的单调性并证明;
(2)解不等式f(x)+f(x﹣2)≤3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com