
【题目】设![]() 是正整数.在一个十进制
是正整数.在一个十进制![]() 位数的各位数字中,若含有数字8,则在每个数字8的前一位数字就不能是数字3(即不能出现38字样).试求出所有这样的
位数的各位数字中,若含有数字8,则在每个数字8的前一位数字就不能是数字3(即不能出现38字样).试求出所有这样的![]() 位数的个数.
位数的个数.
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】设有限数列![]() ,定义集合
,定义集合![]() 为数列
为数列![]() 的伴随集合.
的伴随集合.
(Ⅰ)已知有限数列![]() 和数列
和数列![]() .分别写出
.分别写出![]() 和
和![]() 的伴随集合;
的伴随集合;
(Ⅱ)已知有限等比数列![]() ,求
,求![]() 的伴随集合
的伴随集合![]() 中各元素之和
中各元素之和![]() ;
;
(Ⅲ)已知有限等差数列![]() ,判断
,判断![]() 是否能同时属于
是否能同时属于![]() 的伴随集合
的伴随集合![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(1)求![]() 与
与![]() 的极坐标方程;
的极坐标方程;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() ,E为PD的中点,点F在PC上,且
,E为PD的中点,点F在PC上,且![]() .
.
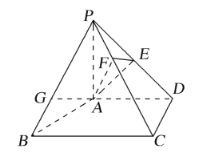
(1)求证:平面![]() 平面PAD;
平面PAD;
(2)求二面角F-AE-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线C顶点在坐标原点,焦点F在Y轴的非负半轴上,点![]() 是抛物线上的一点.
是抛物线上的一点.

(1)求抛物线C的标准方程
(2)若点P,Q在抛物线C上,且抛物线C在点P,Q处的切线交于点S,记直线 MP,MQ的斜率分别为k1,k2,且满足![]() ,当P,Q在C上运动时,△PQS的面积是否为定值?若是,求出△PQS的面积;若不是,请说明理由.
,当P,Q在C上运动时,△PQS的面积是否为定值?若是,求出△PQS的面积;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计,某蔬菜基地西红柿亩产量的增加量![]() (百千克)与某种液体肥料每亩使用量
(百千克)与某种液体肥料每亩使用量![]() (千克)之间的对应数据的散点图,如图所示.
(千克)之间的对应数据的散点图,如图所示.

(1)依据数据的散点图可以看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(若
并加以说明(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)求![]() 关于
关于![]() 的回归方程,并预测液体肥料每亩使用量为
的回归方程,并预测液体肥料每亩使用量为![]() 千克时,西红柿亩产量的增加量约为多少?
千克时,西红柿亩产量的增加量约为多少?
附:相关系数公式 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年3月21日是世界睡眠日,良好的睡眠状况是保持身体健康的重要基础.为了做好今年的世界睡眠日宣传工作,某社区从本辖区内同一年龄层次的人员中抽取了100人,通过问询的方式得到他们在一周内的睡眠时间(单位:小时),并绘制出如右的频率分布直方图:
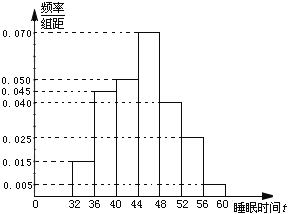
(Ⅰ)求这100人睡眠时间的平均数![]() (同一组数据用该组区间的中点值代替,结果精确到个位);
(同一组数据用该组区间的中点值代替,结果精确到个位);
(Ⅱ)由直方图可以认为,人的睡眠时间![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 近似地等于样本平均数
近似地等于样本平均数![]() ,
,![]() 近似地等于样本方差
近似地等于样本方差![]() ,
,![]() .假设该辖区内这一年龄层次共有10000人,试估计该人群中一周睡眠时间位于区间(39.2,50.8)的人数.
.假设该辖区内这一年龄层次共有10000人,试估计该人群中一周睡眠时间位于区间(39.2,50.8)的人数.
附:![]() .若随机变量
.若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com