已知二阶矩阵M有特征值
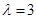
及对应的一个特征向量
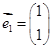
,并且矩阵M对应的变换将点
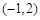
变换成
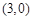
,求矩阵M.
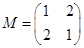
.
试题分析:先设矩阵
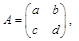
这里
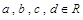
,由二阶矩阵
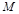
有特征值
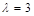
,以及对应的一个特征向量
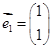
,及矩阵
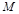
对应的变换将
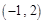
变换成
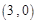
,得到关于
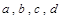
的方程组,即可求得矩阵
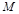
.
试题解析:设矩阵
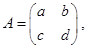
这里
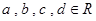
,则
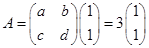
,故
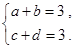

,故
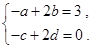
联立以上两方程组解得
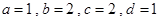
,故
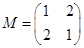
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知二阶矩阵
M有特征值

及对应的一个特征向量

,且
M
=

.求矩阵
M.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知a,b
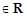
,若
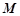
=
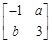
所对应的变换T
M把直线2x-y=3变换成自身,试求实数a,b.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
.已知矩阵
A=
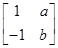
,
A的一个特征值
λ=2,其对应的特征向量是
α1=
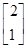
.设向量
β=
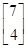
,试计算
A5β的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
求矩阵A=
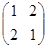
的特征值
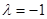
所对应的一个特征向量。
查看答案和解析>>

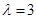 及对应的一个特征向量
及对应的一个特征向量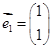 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点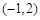 变换成
变换成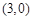 ,求矩阵M.
,求矩阵M. 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案