
 、
、 、
、 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 =(1,2).
=(1,2). |=2
|=2 ,且
,且 ∥
∥ ,求
,求 的坐标.
的坐标. |=
|= ,且
,且 +2
+2 与2
与2 -
- 垂直,求
垂直,求 与
与 的夹角θ
的夹角θ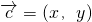 (1分)
(1分) ∥
∥ 且|
且| |=2
|=2
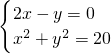 ,(3分)
,(3分) =(2,4)或
=(2,4)或 =(-2,-4)(6分)
=(-2,-4)(6分) +2
+2 )⊥(2
)⊥(2 -
- )
) +2
+2 )•(2
)•(2 -
- )=0(8分)
)=0(8分) 2+3
2+3 •
• -2
-2 2=0
2=0 |2+3|
|2+3| |•|
|•| |cosθ-2|
|cosθ-2| |2=0
|2=0 ×
× cosθ-2×
cosθ-2× =0
=0 的坐标,利用它与
的坐标,利用它与 平行以及它的模等于2
平行以及它的模等于2 ,待定系数法求出
,待定系数法求出 的坐标.
的坐标. +2
+2 与2
与2 -
- 垂直,数量积等于0,求出夹角θ的余弦值,再利用夹角θ的范围,求出此角的大小.
垂直,数量积等于0,求出夹角θ的余弦值,再利用夹角θ的范围,求出此角的大小.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届安徽省高一下学期期中考试数学试卷(解析版) 题型:解答题
已知: 、
、 、
、
 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 =(1,2)
=(1,2)
(1)若|  |
| ,且
,且 ,求
,求 的坐标;
的坐标;
(2)若|  |=
|= 且
且 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角 .
.
查看答案和解析>>
科目:高中数学 来源:2014届山西省高一6月月考理科数学试卷(解析版) 题型:解答题
已知: 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 =(1,2)
=(1,2)
⑴若| |
| ,且
,且 ,求
,求 的坐标;
的坐标;
⑵若| |=
|= 且
且 与
与 垂直,求
垂直,求 与
与 的夹角θ.
的夹角θ.
查看答案和解析>>
科目:高中数学 来源:山东省2013届高一下学期期末考试数学 题型:解答题
( 12分)已知: 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 =(1,2)
=(1,2)
(1)( 6分)若| |
| ,且
,且 ,求
,求 的坐标;
的坐标;
(2)( 6分)若| |=
|= 且
且 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com