
分析 由题意知本题是一个古典概型,用组合数表示出试验发生所包含的所有事件数,满足条件的事件分为两种情况①先摸出红球,再摸出红球,②先摸出白球,再摸出白球,根据古典概型公式得到结果.
解答 解:由题意知本题是一个古典概型,
∵试验发生所包含的所有事件数是C51C51=25,
满足条件的事件分为两种情况
①先摸出红球,P红=C21,再摸出红球,P红红=C21C21=4;
②先摸出白球,P白=C31,再摸出白球,P白白=C31C31=9,
∴P=$\frac{4+9}{25}$=$\frac{13}{25}$.
故答案为:$\frac{13}{25}$
点评 古典概型要求能够列举出所有事件和发生事件的个数,实际上本题可以列举出所有事件,概率问题同其他的知识点结合在一起,实际上是以概率问题为载体,主要考查的是另一个知识点.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | y=2x | B. | y=${log}_{\frac{1}{2}}$x | C. | y=x-1 | D. | y=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y全不为0,则x2+y2≠0” | |
| B. | 若命题$p:?{x_0}∈R,{x_0}^2-{x_0}+1<0$,则?p:?x∉R,x2-x+1≥0 | |
| C. | 若命题“p或q”为真命题,则命题p和命题q均为真命题 | |
| D. | “x>3”是“x>2”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | [-1,0) | C. | (-1,+∞) | D. | {x|x≥-1,且x≠0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y|1≤y<7} | B. | {y|1≤y≤7} | C. | {1,3,5,7} | D. | {1,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪[3,+∞) | B. | [1,3] | C. | $[{\frac{3}{2},3}]$ | D. | $({-∞,\frac{3}{2}}]∪[{3,+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
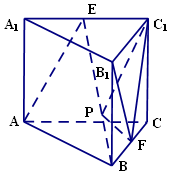 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com