
【题目】从某商场随机抽取了2000件商品,按商品价格(元)进行统计,所得频率分布直方图如图所示.记价格在![]() ,
,![]() ,
,![]() 对应的小矩形的面积分别为
对应的小矩形的面积分别为![]() ,且
,且![]() .
.
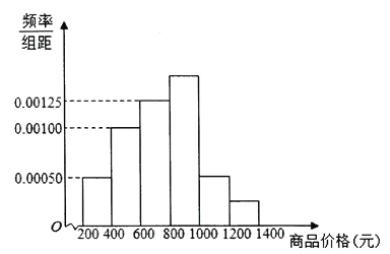
(1)按分层抽样从价格在![]() ,
,![]() 的商品中共抽取6件,再从这6件中随机抽取2件作价格对比,求抽到的两件商品价格差超过800元的概率;
的商品中共抽取6件,再从这6件中随机抽取2件作价格对比,求抽到的两件商品价格差超过800元的概率;
(2)在清明节期间,该商场制定了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表,如果你是消费者,你会选择哪种方案?为什么?(同一组中的数据用该组区间中点值作代表)
商品价格 |
|
|
|
|
|
|
优惠(元) | 30 | 50 | 140 | 160 | 280 | 320 |
【答案】(1)![]() ;(2)方案一,原因见解析
;(2)方案一,原因见解析
【解析】
(1)根据频率和为1的性质,计算得出![]() ,再得出价格在
,再得出价格在![]() ,
,![]() 的频率,由分层抽样的性质得出
的频率,由分层抽样的性质得出![]() 和
和![]() 抽取的件数,得出
抽取的件数,得出![]() 件中抽两件的所有情况,从中得出符合题意的情况,由古典概型概率公式计算即可;
件中抽两件的所有情况,从中得出符合题意的情况,由古典概型概率公式计算即可;
(2)由频率分布直方图得出各组的频率,分别计算出两种方案优惠的价钱的平均值,即可作出判断.
(1)根据频率和为1的性质知![]() ,
,
又![]() ,得到
,得到![]() ;
;
价格在![]() 的频率为
的频率为![]() ,价格在
,价格在![]() 的频率为
的频率为![]() ;
;
按分层抽样的方法从价格在![]() ,
,![]() 的商品中抽取6件
的商品中抽取6件
则在![]() 上抽取4件,记为
上抽取4件,记为![]() ;在
;在![]() 上抽取2件,记为
上抽取2件,记为![]() ;
;
现从中抽出2件,所有可能情况为:![]() ,共计15种;
,共计15种;
其中符合题意的有![]() ,共8种;
,共8种;
因此抽到的两件商品价格差超过800元的概率为![]() .
.
(2)对于方案一,优惠的价钱的平均值为:
![]() 元;
元;
对于方案二,优惠的价钱的平均值为:
![]() 元;
元;
因为![]() ,所以选择方案一更好.
,所以选择方案一更好.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】随着人民生活水平的日益提高,某小区居民拥有私家车的数量与日俱增.由于该小区建成时间较早,没有配套建造地下停车场,小区内无序停放的车辆造成了交通的拥堵.该小区的物业公司统计了近五年小区登记在册的私家车数量(累计值,如147表示2016年小区登记在册的所有车辆数,其余意义相同),得到如下数据:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
数量 | 37 | 104 | 147 | 196 | 216 |
(1)若私家车的数量![]() 与年份编号
与年份编号![]() 满足线性相关关系,求
满足线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该小区的私家车数量;
的线性回归方程,并预测2020年该小区的私家车数量;
(2)小区于2018年底完成了基础设施改造,划设了120个停车位.为解决小区车辆乱停乱放的问题,加强小区管理,物业公司决定禁止无车位的车辆进入小区.由于车位有限,物业公司决定在2019年度采用网络竞拍的方式将车位对业主出租,租期一年,竞拍方案如下:①截至2018年己登记在册的私家车业主拥有竞拍资格;②每车至多中请一个车位,由车主在竞拍网站上提出申请并给出自己的报价;③根据物价部门的规定,竞价不得超过1200元;④申请阶段截止后,将所有申请的业主报价自高到低排列,排在前120位的业主以其报价成交;⑤若最后出现并列的报价,则以提出申请的时间在前的业主成交,为预测本次竞拍的成交最低价,物业公司随机抽取了有竞拍资格的40位业主,进行了竞拍意向的调查,并对他们的拟报竞价进行了统计,得到如图频率分布直方图:

(i)求所抽取的业主中有意向竞拍报价不低于1000元的人数;
(ii)如果所有符合条件的车主均参与竞拍,利用样本估计总体的思想,请你据此预测至少需要报价多少元才能竞拍车位成功?(精确到整数)
参考公式及数据:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: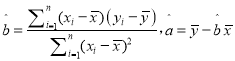 ;
;.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 45 | 75 | 90 | 60 | 30 |
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);

(2)把评分不低于70分的用户称为“评分良好用户”,能否有![]() 的把握认为“评分良好用户”与性别有关?
的把握认为“评分良好用户”与性别有关?
参考附表:
|
|
|
| |
|
|
|
|
|
参考公式 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高一期中考试结束后,从高一年级1000名学生中任意抽取50名学生,将这50名学生的某一科的考试成绩(满分150分)作为样本进行统计,并作出样本成绩的频率分布直方图(如图).
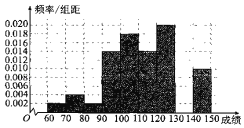
(1)由于工作疏忽,将成绩[130,140)的数据丢失,求此区间的人数及频率分布直方图的中位数;(结果保留两位小数)
(2)若规定考试分数不小于120分为优秀,现从样本的优秀学生中任意选出3名学生,参加学习经验交流会.设X表示参加学习经验交流会的学生分数不小于130分的学生人数,求X的分布列及期望;
(3)视样本频率为概率.由于特殊原因,有一个学生不能到学校参加考试,根据以往考试成绩,一般这名学生的成绩应在平均分左右.试根据以上数据,说明他若参加考试,可能得多少分?(每组数据以区问的中点值为代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com